Many tasks in artificial intelligence (AI) can be formulated as search problems, where the goal is to find a solution by exploring possible states (state space). For this chapter, an understanding in Data Structures and Algorithms is recommended.
Defining a search problem
A search problem involves moving from an initial state to a goal state using a set of operators, while considering the path cost function.
Examples of search problems
| Task | Initial State | Goal State | Operators (Actions) | Path Cost (Quality) |
|---|---|---|---|---|
| Driving | Start location (e.g., Arad) | Destination (e.g., Bucharest) | Driving between cities | Distance, time, fuel cost |
| Chess | Initial board setup | Checkmate position | Possible legal moves | Number of moves, board advantage |
| Logical Reasoning | Set of facts and rules | Answer to a query | Applying inference rules | Number of steps, computational cost |
Components of a search problem
A search problem is formally defined by four key components:
- Initial State
- The starting point of the problem.
- Example: In a navigation problem, the initial state is the starting location.
- Goal State
- The desired outcome of the search.
- Can be defined explicitly (e.g., “Reach Bucharest”) or implicitly (e.g., “Find a checkmate position in chess”)
- Operators (Actions)
- A set of possible actions transforming one state to another
- Example: In chess, moving a knight from one square to another is an operator
- Path Cost Function
- Measures the quality of a solution (lower cost = better solution)
- Example: In driving, cost can be distance, time, or fuel
- State space: A state space is the set of all possible states that can be reached in a given problem by applying a set of operators (actions) starting from an initial state.
Searching - Example
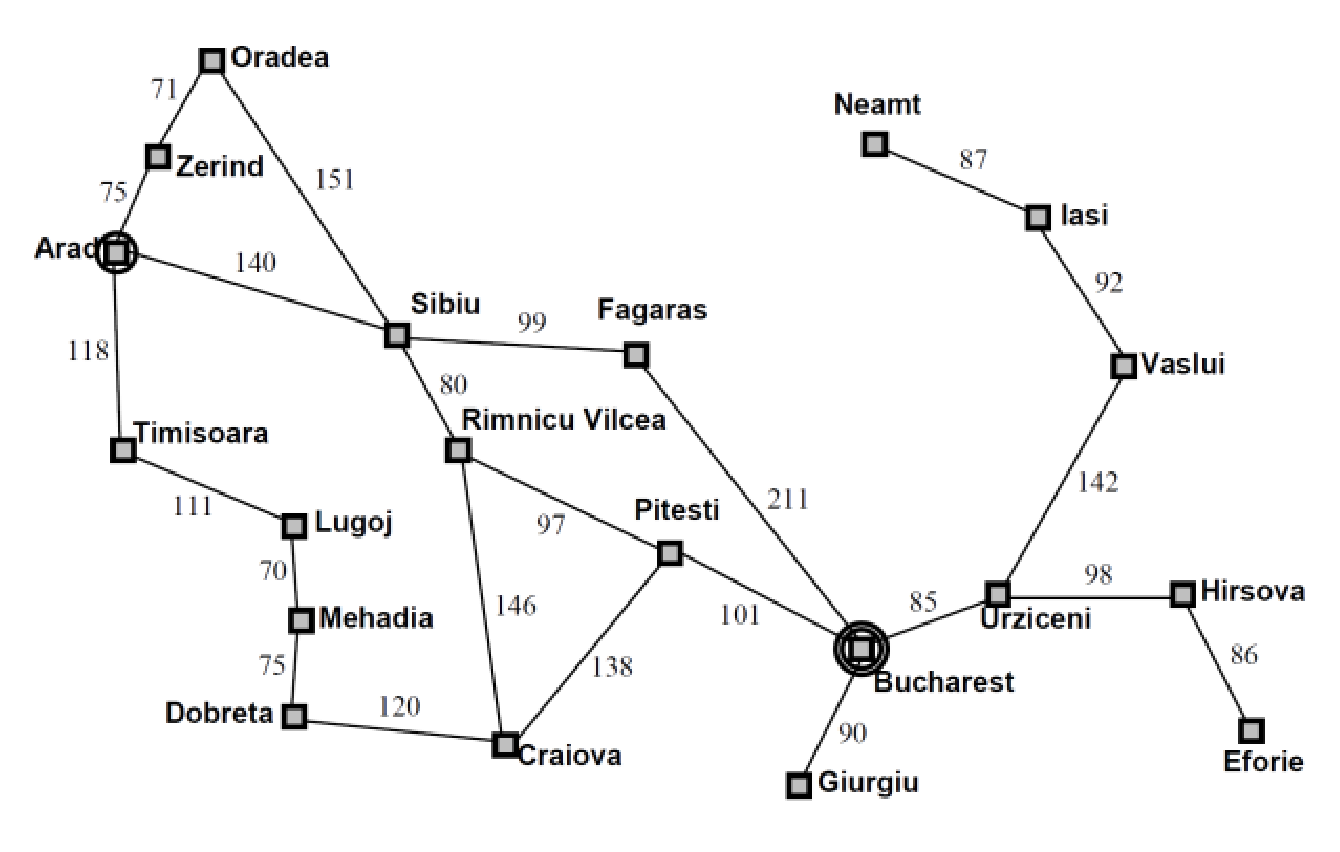
Problem formulation
The solution to a search problem is a sequence of actions that leads from the initial state to the goal state while minimising cost. The process follows these steps:
- Initial state: Arad
- Goal state: Bucharest
- Operators (Actions): A set of possible actions transforming one state to another. E.g. Arad → Zerind, Arad → Sibiu
- Path cost function: Distance traveled
Choosing states and actions (Abstraction)
Real problems are too complex, to solve them we need to abstract them. Which is, to simplify them by removing the unnecessary details and choose suitable actions.
- Remove unnecessary details
- Not all real-world details are important for solving a problem. When abstracting a problem, we ignore irrelevant factors and focus only on what affects the solution.
- E.g. we ignore the weather, travel companion, scenery; they are irrelevant to the task of finding a path to Bucharest.
- The action need to be suitable
- To keep the problem manageable, actions should be abstracted into meaningful steps rather than unnecessary details.
- E.g. “Turn the steering wheel to the left by 5 degrees” is not appropriate
The level of abstraction must be appropriate (valid and useful).
- (Abstract) state = set of real states
- (Abstract) action = complex combination of real actions
- (Abstract) solution = a real path that is solution in the real world
Types of problem formulation
Incremental Formulation (State-Space Search Approach)
- The solution is built step by step, exploring the search space incrementally.
- At each step, the current state is expanded by applying an operator (action), leading to a new state.
- The process continues until the goal state is reached.
Example:
-
Route Finding Problem (Arad to Bucharest)
- Start at Arad.
- Choose a valid move (e.g., drive to Sibiu).
- Continue selecting moves until reaching Bucharest.
-
Common Algorithms:
- Uninformed Search: BFS (Breadth-First Search), DFS (Depth-First Search), Uniform-Cost Search
- Informed Search: A* (A-star), Greedy Best-First Search
Complete-State Formulation (Constraint Satisfaction Approach)
- The problem is viewed as a single state representation, and the solver attempts to find a complete solution directly.
- The entire problem state is considered at once, with constraints guiding the search for a solution.
- Instead of incremental steps, solutions are found by ensuring all constraints are satisfied.
Example:
-
8-Queens Problem (placing 8 queens on a chessboard so that no two attack each other):
- Instead of placing one queen at a time, the problem is treated as a complete board configuration.
- The solver finds a valid board arrangement that satisfies all constraints.
-
Common Techniques:
- Backtracking Search
- Constraint Propagation
- Optimisation Methods
Search strategy
A search strategy defines which node from the fringe is the most promising and should be expanded next. We keep the nodes in the fringe ordered based on the search strategy and always expand the first one. (i.e. the best one)
Definitions
- Expanded list
- The expanded list contains all the nodes (states) that have already been visited and expanded
- Fringe list
- The fringe list contains all the nodes that have been discovered but not yet expanded
- Branching factor ()
- The branching factor refers to the average number of child nodes (successor states) that each node is the search tree can have.
Evaluation criteria
- Completeness
- A search algorithm is complete if it always finds a solution (if one exists) in the state space. In another word, the search algorithm guarantees finding a solution if one exists.
- **Optimality
- A search algorithm is optimal if it always finds an optimal (least cost path) solution.
- Time complexity
- How long does it take to find the solution?
- Space complexity
- The amount of memory (computational space) required to store the data structures needed for the search process, and any additional storage used by the algorithm.
Algorithm complexities
Time and space complexity are measured in terms of:
- Maximum branching factor ()
- Maximum branching factor of the search tree (we can assume that it is finite). Which is, the largest number of child nodes that any node in the search tree can have. It defines the upper limit on the number of children a node can generate.
- Depth ()
- The depth of the optimal (least cost) solution
- Maximum depth ()
- Maximum depth of the state space (can be finite or not finite i.e. ∞)
Types of search methods
An informed search can find the goal faster than an uninformed search algorithm, provided that the heuristic function is well-defined.
Uniformed (blind) search
The algorithm has no additional knowledge beyond the problem definition (initial state, goal state, and operators).
The uniformed search algorithms:
- Breadth-First Search (BFS)
- Depth-First Search (DFS)
- Depth-limited search
- Iterative Deepening Search (IDS)
- Uninformed Cost Search (UCS)
Informed (heuristic search)
The algorithm uses extra knowledge (heuristics) to guide the search towards the goal more efficiently. It receives a state at its input and estimates how close it is to the goal.
The informed search algorithms:
AI AI_Algorithm Problem_Solving Uninformed_Search Informed_Search
Reference: