Abstract data type:

ADT - Binary Tree

Related algorithm

Range Query in BST

Data_Structure Tree Binary_Tree Binary_Search_Tree

Binary search tree or BST is a tree data structure that organise data in a sorted manner, it is an ordered binary tree. The hierarchical structure allows for efficient searching, insertion, and deletion on the data stored in the tree.

graph TB;
A((8))-->B((3))
A-->C((10))
B-->D((1))
B-->E((6))
C-->F((9))
C-->G((14))
E-->H((4))
E-->I((7))

Properties

Each BST node has at most two children
A node can have a left child and a right child, with the left child containing values less than the parent node; the right child containing the values greater than the parent
The left subtree of a node contains only nodes with keys lesser than the node’s key; the right subtree of a node contains only nodes with keys greater than the node’s key (performing binary search is very efficient in BST)
There must be no node with the same key
Self-balancing BST
- BST can be balanced or unbalanced depending on the order of inserting nodes.
- A self-balancing BST is a BST that automatically keeps its height small in face of arbitrary item insertions or deletions. For self-balanced binary trees, the height is defined to be log n in the number n of items. AVL trees and red-black trees are self-balancing BSTs.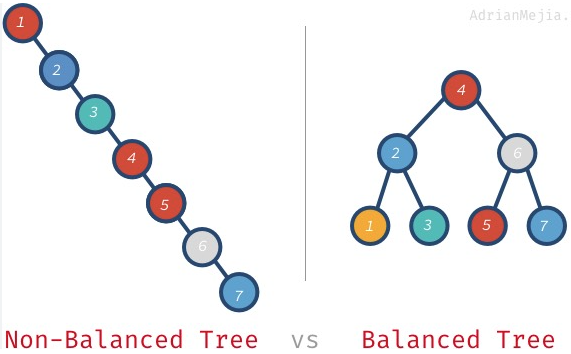
Binary Search Tree with Duplicate Values
- A classic BST will not allow duplicate keys, keys in BST are in strict increasing order. However, we have a variation of BST that allows duplications. It follows the property either key(left descendant) $\leq$ key(node) $<$ key (right descendant) OR key(left descendant) < key(node) $\leq$ key (right descendant) OR using a list to store duplicate values.

Pros and cons

Advantage
- Efficient searching: average $O (lo g n)$ time for searching, worst-case $O (n)$ time for unbalanced BST
- Ordered structure: elements are sorted in order, making it easy to find the next or previous element
- Dynamic insertion and deletion: elements can be added or removed efficiently in balanced BST
Disadvantage
- Not self-balancing: unbalanced BSTs can lead to poor performance for searching and insertion resulting in $O (n)$ time
- Memory overhead: BST requires additional memory to store pointers to child node

Implementation

Insertion

A new key is always inserted at the leaf to maintain the property of the BST. Start searching for a key from the root until reaches a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.

Time complexity

The time complexity of insertion operation takes $O (h)$ time where h is the height of the BST, because we are using comparison to skip about half of the tree. The overall time complexity is $O (lo g n)$ . In the worst-case, the height of a skewed tree may become n, and the time complexity of insertion operation may become $O (n)$ .

Implementation

Start at the root of the tree
Compare the value of the node to be inserted with the value of the current node
If the value of the node to be inserted is less than the value of the current node, move to the left child
If the left child is null, insert the new node as the left child of the current node
If the value of the node to be inserted is greater than the value of the current node, move to the right child
If the right child is null, insert the new node as the right child of the current node
Repeat steps 3-6 until a suitable position for insertion is found

public void insert(Node node) {  
    root = insertHelper(root, node);  
}  
  
private Node insertHelper(Node root, Node node) { 
	
	  int data = node.data;  
	  
	  //check the root of current subtree
    if (root == null) {  
		//indicating an empty subtree, the new node is assigned to                  //the root of this subtree
        root = new Node(node.data);
        //return the updated root
        return root;  
    }  
    
    if (data < root.data) {  
	    //update the left child of the current node with the result of 
	    //the insertion operation
        root.left = insertHelper(root.left, node);  
    } else {  
        root.right = insertHelper(root.right, node);  
    }  
    //return the root of the subtree
    return root;  
}

Searching

Search for a key in a given BST. We start from the root and compare value to be searched with the value of the root, if it is equal we are done with the search, if it is smaller we go to the left subtree, because we know every node on the left are smaller than the current root, go to the right otherwise.

Time complexity

In the best-case, a balanced BST, the time complexity of searching is $O (lo g n)$ , where the $n$ is the number of nodes in the tree. This efficiency is achieved by halving the search space at each level by going to either left or right. In the worse-case, an unbalanced BST, the time complexity for searching can be $O (n)$ if the tree is completely skewed, the nodes are arranged in a linear fashion and the searching is similar to going through a linked list.

Implementation

Start at the root of the tree
Compare the value of the key to be searched with the value of the current node.
If the value of the key is equal to the value of the current node, return true (indicating that the key is found)
If the value of the key is less than the value of the current node, move to the left child
If the value of the key is greater than the value of the current node, move to the right child
Repeat steps 2-5 until the key is found or until reaching a leaf node
If the key is not found after traversing the tree, return false

public boolean search(int target) {  
    return searchHelper(root, target);  
}  
  
private boolean searchHelper(Node root, int target) {  
    if (root == null) {  
        return false;  
    }  
    if (root.data == target) {  
        return true;  
    }  
    //target is in the right subtree
    if (root.data < target) {  
       return searchHelper(root.right, target);  
    }  
    if (root.data > target) {  
        return searchHelper(root.left, target);  
    }  
    return false;  
}

Deletion

The deletion of a node can be in three of the situations:

Delete a leaf node
- Assign the node to null
Delete a node with single child
- Replace the node to be deleted with its child
Delete a node with both children
- We have two ways of approaching this
- We find the minimum key of the right subtree of the node to be deleted, and assign the minimum key to the node that we want to delete, and we delete the node with the minimum key in the subtree.
- OR we find the maximum key of the left subtree of the node to be deleted, and assign the maximum key to the node that we want to delete, and we deleted the node with the maximum key in the subtree.

Before deletion: We want to delete the node with key 3, we replace the node 3 with the minimum value of the node from its right subtree.

graph TB;
A((8))-->B((3))
A-->C((10))
B-->D((1))
B-->E((6))
C-->F((9))
C-->G((14))
E-->H((4))
E-->I((7))

After deletion:

graph TB;
A((8))-->B((4))
A-->C((10))
B[4]-->D((1))
B-->E((6))
C-->F((9))
C-->G((14))
E-->I((7))

style B fill:#ffcccc,stroke:#333,stroke-width:1px,stroke-dasharray: 5, 5;

Time complexity

In the best-case, a balanced BST, the deletion involves searching for the node to be deleted, which takes a $O (lo g n)$ time, and the node to be deleted is a leaf node. The time complexity is $O (lo g n)$ . In an average case, a balanced BST, the deletion involves searching for the node to be deleted, takes a $O (lo g n)$ time. The node has two children, we need to find the minimum value of the node from its right subtree, this process takes $O (lo g n_{s u b})$ time where $n$ is the number of nodes in the right subtree. Now we have to delete the minimum node from the right subtree, this process takes $O (lo g n_{s u b})$ time. The total complexity can be described as $O (lo g n) + O (lo g n_{s u b}) + O (lo g n_{s u b}) = O (lo g n)$ In the worst-case, an unbalanced BST, the deletion involves searching for the node to be deleted takes a $O (n)$ time, since the searching dominates the runtime, the overall complexity is $O (n)$ .

Implementation

This implementation employs replacing the node to be deleted with the greatest value from its left subtree.

Search through the BST to find the node to be deleted
Check if the node to be deleted has only a child or no child, if yes replace the node to be deleted with its child, or dereference the node
If the node has two children, employ either left maximum or right minimum approach (in the following example we are using the left maximum approach)
Find the left maximum value and assign the value to the node to be deleted
Remove the left maximum node

public void delete(int key) {  
    this.root = deleteHelper(root, key);  
}  
  
private Node deleteHelper(Node root, int key) {  
    if (root == null) return null;  
	
	// search for the node to be deleted
    if (key < root.data)  
        root.left = deleteHelper(root.left, key);  
    else if (key > root.data)  
        root.right = deleteHelper(root.right, key);  
    else {  
        // we found the node to be deleted  
        // check if the node has child
		// if yes, replace the target node with its child
		// if no, dereference the node (assign with null)        
		if (root.left == null)  
            return root.right;  
        else if (root.right == null)  
            return root.left;  
            
        // if the node to be deleted has two children,  
        // assign the value of the greatest node from the 
        // left subtree to the node to be deleted        
        root.data = greatestValue(root.left);  
        
        // delete the greatest node from the left subtree  
        root.left = deleteHelper(root.left, root.data);  
    }  
    return root;  
}
 
private int greatestValue(Node root) {  
    int greatestValue;  
    // in this subtree, find the greatest value  
    while (root.right != null) {  
        root = root.right;  
    }  
    greatestValue = root.data;  
    return greatestValue;  
}

Display

Display the BST using in-order traversal, in ascending order of the key values. The left most node (smallest key value) will be printed first.

Time complexity

The display operation takes a time complexity of $O (n)$ as it has to go through each node on the tree once.

Implementation

Start at the root of the tree
Check if the current node is not null
Recursively traverse the left subtree with the left child of the current node
Print the data of the current node
Recursively traverse the right subtree with the right child of the current node

private void displayTreeHelper(Node root) {  
    if (root == null) {  
        return;  
    }  
    
    displayTreeHelper(root.left);  
    System.out.println(root.data + " ");  
    displayTreeHelper(root.right);  
}

Back to parent node: ADT - Binary Tree

Reference

Computer Science Wiki

Explorer

Binary Search Tree (BST)

Properties

Pros and cons

Implementation

Insertion

Time complexity

Implementation

Searching

Time complexity

Implementation

Deletion

Time complexity

Implementation

Display

Time complexity

Implementation

Graph View

Table of Contents

Backlinks