1R Algorithm

The 1R algorithm (short for “One Rule”) is a simple, rule-based machine learning classifier used for classification. It creates a single rule for each feature and then selects the rule with the lowest error rate to make predictions.

How it works

1. For each attribute, create rules that map attribute values to the most frequent class label for that value (if there is a tie, chose a random class)
2. Calculate the error rate of each rule
3. Select the rule (and corresponding attribute) with the lowest total error
4. Use this rule as the final model to classify all future instances

Example study

Given the dataset: Attributes: Outlook, Temp, Humidity, Windy
Class label: Play (yes or no)

Outlook	Temp	Humidity	Windy	Play
Sunny	Hot	High	False	No
Sunny	Hot	High	True	No
Overcast	Hot	High	False	Yes
Rainy	Mild	High	False	Yes
Rainy	Cool	Normal	False	Yes
Rainy	Cool	Normal	True	No
Overcast	Cool	Normal	True	Yes
Sunny	Mild	High	False	No
Sunny	Cool	Normal	False	Yes
Rainy	Mild	Normal	False	Yes
Sunny	Mild	Normal	True	Yes
Overcast	Mild	High	True	Yes
Overcast	Hot	Normal	False	Yes
Rainy	Mild	High	True	No

Create 1R rules for each attribute

Attribute Outlook

• Sunny → 5 samples → 3 No, 2 Yes → Predict No (majority)
• Overcast → 4 samples → 4 Yes, 0 No → Predict Yes
• Rainy → 5 samples → 3 Yes, 2 No → Predict Yes

Rule

If Outlook = Sunny → No  
If Outlook = Overcast → Yes  
If Outlook = Rainy → Yes

Error

• Sunny → 2 Yes misclassified (2/5)
• Overcast → 0 misclassified (0/4)
• Rainy → 2 No misclassified (2/5)

Total errors = 2 + 0 + 2 = 4 out of 14

Attribute Temp

Temp Value	Play = Yes	Play = No	Rule	Errors
Hot	2	2	Predict No (random choice)	2
Mild	4	2	Predict Yes	2
Cool	3	1	Predict Yes	1

Rule

If Temp = Hot → No  
If Temp = Mild → Yes  
If Temp = Cool → Yes

Total Errors = 2 + 2 + 1 = 5

Attribute Humidity

Humidity Value	Play = Yes	Play = No	Rule	Errors
High	3	4	Predict No	3
Normal	6	1	Predict Yes	1

Rule

If Humidity = High → No  
If Humidity = Normal → Yes

Total Errors = 3 + 1 = 4

Attribute Windy

Windy Value	Play = Yes	Play = No	Rule	Errors
False	6	2	Predict Yes	2
True	3	3	Predict No (random choice)	3

Rule

If Windy = False → Yes  
If Windy = True → No

Total Errors = 2 + 3 = 5

Final decision

Attribute	Total Errors
Outlook	4
Temp	5
Humidity	4
Windy	4
Since Outlook, Humidity, and Windy all tie with the fewest errors (4), 1R selects one — we’ll pick Outlook.

Final 1R rule (based on outlook)

This rule becomes the final classifier for new examples.

If Outlook = Sunny → No  
If Outlook = Overcast → Yes  
If Outlook = Rainy → Yes

Handling examples with missing values (general topic)

The 1R algorithm and other classification algorithms handle missing values in two main ways depending on implementation:

Method 1: Ignore instances with missing values

When generating rules for a particular attribute, only use rows where that attribute is not missing.

• Pros
  • Easy to implement
  • Keeps logic clean per attribute
• Cons
  • Sometimes these instances are useful

Method 2: Treat missing as a separate value

Instead of discarding rows with missing values or filling them in, 1R treats the missing value (?) as just another category of the attribute. This assumes that the absence of a value itself might be meaningful. For example, normally, the Outlook attribute has 3 possible values: Sunny, Overcast, and Rainy. But now, suppose some rows have Outlook = ? (missing), we treat ? as a fourth value. So the 1R rule for Outlook will create 4 rules, like:

If Outlook = Sunny → ...
If Outlook = Overcast → ...
If Outlook = Rainy → ...
If Outlook = ? → ...

Method 3: Replace (impute) missing value

This method fills in missing values using values from the dataset — a process called imputation. There are two common ways to do it:

Replace with most common value (global mode)

Replace missing values in attribute A with the most frequent value of A across all training data. Let’s say the attribute is Temp and these are the values in the dataset:

Temp	Count
Hot	4
Mild	6 ← most common
Cool	4
So, any missing value in Temp is replaced with “Mild”.

Replace with most common value within the same class

Replace missing values in attribute A with the most common value of A among training examples that have the same class as the example with the missing value.

Suppose you have a row like

Outlook = Sunny, Temp = ?, Play = Yes

To fill in Temp, look at only those rows where Play = Yes and find the most frequent Temp value in that subset.

Assume:

Temp (where Play = Yes)	Count
Mild	4 ← most common among “Yes”
Cool	3
Hot	2
So you would replace ? with “Mild”.

Dealing with numeric attributes

The 1R algorithm works by making one rule per attribute, and each rule is based on discrete (categorical) values. 1R can’t directly handle continuous numeric values — it needs categories like low, medium, high.

Discretisation

Discretisation is the process of converting numeric attributes into nominal (categorical) values by dividing them into ranges.

Example

Given the training dataset:

Outlook	Temp	Humidity	Windy	Play
Sunny	85	85	False	No
Sunny	80	90	True	No
Overcast	83	86	False	Yes
Rainy	70	96	False	Yes
Rainy	68	80	False	Yes
Rainy	65	70	True	No
Overcast	64	65	True	Yes
Sunny	72	95	False	No
Sunny	69	70	False	Yes
Rainy	75	80	False	Yes
Sunny	75	70	True	Yes
Overcast	73	90	True	Yes
Overcast	81	75	False	Yes
Rainy	71	91	True	No

Step 1: Sort the Data by Temperature

Sort the training examples in increasing order according to the value of the numeric attribute, and their corresponding class labels (play = yes/no):

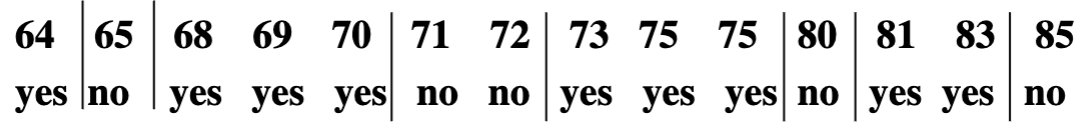
Step 2: Find breakpoints where the class changes

Look for places where the class (yes/no) flips between two adjacent temperature values.

• From 64: yes to 65: no → class change ⇒ breakpoint between 64 & 65
• From 65: no to 68: yes → class change ⇒ breakpoint between **65 & 68
• From 70: yes to 71: no → class change ⇒ breakpoint between 70 & 71
• From 72: no to 73: yes → class change ⇒ breakpoint between 72 & 73
• Etc.

We place breakpoints halfway between those temperature values:

• Between 64 and 65 → 64.5
• Between 65 and 68 → 66.5
• Between 70 and 71 → 70.5
• Etc.

Step 3: Create rules based on intervals

Now, using these breakpoints, we divide the temperature range into intervals:

if temperature < 64.5           → play = yes
if 64.5 ≤ temperature ≤ 65.5    → play = no
if 65.5 < temperature ≤ 70.5    → play = yes
if 70.5 < temperature ≤ 72.5    → play = no
if 72.5 < temperature ≤ 77.5    → play = yes
if 77.5 < temperature ≤ 80.5    → play = no
if 80.5 < temperature ≤ 84      → play = yes
if temperature ≥ 84             → play = no