Related paradigm:
Algorithm Divide_and_Conquer Sorting_Algorithms Merge_Sort
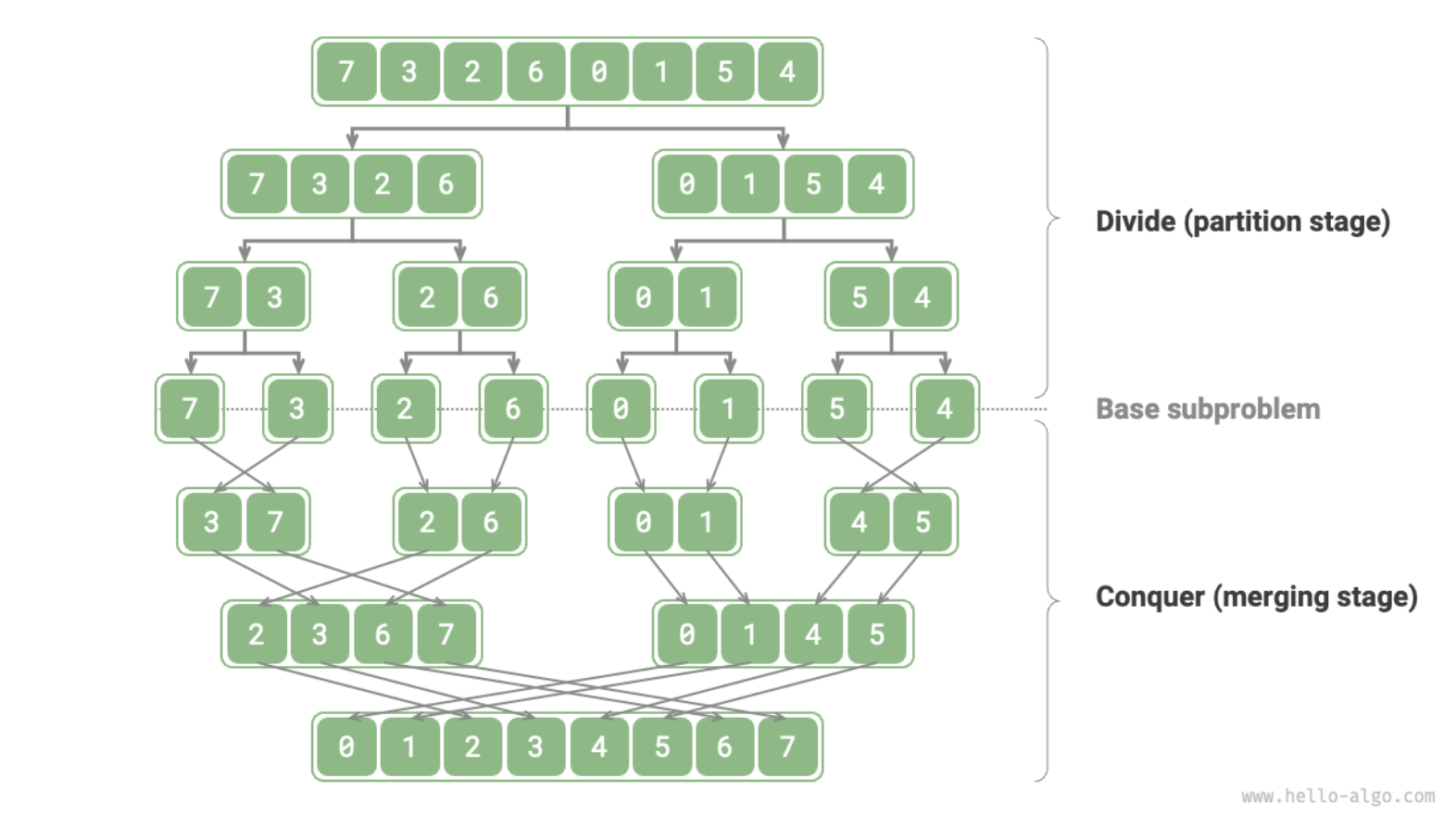
Merge sort is a classic example of the divide and conquer algorithm paradigm.
- Divide
- Divide the unsorted array into two halves
- The base case is reached when the sub-arrays has one or less than one element
- Conquer
- The algorithm recursively sorts the two halves
- Combine
- The algorithm merges two sorted halves into a single sorted array
- It merges two sub-arrays by comparing elements in left array and right array, and copying smaller element back to the original array (ascending order)
- After merging, any remaining elements in left and right array are copied back to the original array
Implementation
public static void main(String[] args) {
int[] arr = {38, 27, 43, 3, 9, 82, 10};
mergeSort(arr, 0, arr.length - 1);
for (int num : arr) {
System.out.print(num + " ");
}
}
private static void mergeSort(int[] arr, int lower, int higher) {
// when sub-array has one or less than one element
if (lower >= higher) {
return ;
}
int mid = (higher+lower)/2;
mergeSort(arr, lower, mid);
mergeSort(arr, mid+1, higher);
merge(arr, lower, mid, higher);
}
private static void merge(int[] arr, int lower, int mid, int higher) {
int n1 = mid - lower + 1;
int n2 = higher - mid;
int[] left = new int[n1];
int[] right = new int[n2];
System.arraycopy(arr, lower, left, 0, n1); // creates left array
System.arraycopy(arr, mid + 1, right, 0, n2); // creates right array
// merge the arrays
// initial indices of the first and second sub-arrays
int i = 0, j = 0;
// initial index of the merged subarray array
int k = lower;
// as long as there is remaining element in either array
while (i < n1 && j < n2) {
if (left[i] <= right[j]) {
arr[k] = left[i];
i++;
} else {
arr[k] = right[j];
j++;
}
k++;
}
// copy the remaining elements of left[], if any
while (i < n1) {
arr[k] = left[i];
i++;
k++;
}
// copy the remaining elements of right[], if any
while (j < n2) {
arr[k] = right[j];
j++;
k++;
}
}Correctness
Base Case:
The base case occurs when the lower index is greater than or equal to the higher index. This means the subarray contains only one or zero element, which is already considered sorted.
Inductive hypothesis
Assume that the mergeSort function correctly sorts any subarray of size k (where k is greater than 1) into ascending order.
Inductive step
Assume that the algorithm works correctly for arrays of size k. We want to show that it also works for arrays of size k+1.
When we call mergeSort on an array of size k+1, the algorithm splits the array into two halves and recursively sorts each half. By our inductive assumption, these halves are correctly sorted.
Then, when the merge function is called, it correctly merges the two sorted halves into a single sorted array. This step is correct because it iteratively selects the smallest element from the two halves and places it in the correct position in the merged array.
Therefore, if the algorithm works correctly for arrays of size k, it also works correctly for arrays of size k+1.
Time complexity
Master theorem
- Divide the problem
- The input list is divided into 2 halves (), each of size ().
- Combine the result
- The merge step uses two pointers iteratively compare elements in two sub-arrays, which takes time. ()
Given the master theorem for divide and conquer in general form: From the evaluated result:
We can obtain the resulting expression: Analyse the master theorem equation:
- Non-recursive part growth rate: ,
- Recursive part growth rate: