Informed Search - A* Search

A* (A-star search) is an informed search algorithm that finds the optimal path from a start node to a goal node. It balances the cost to reach a node and an estimate of the cost to reach the goal.

• Completeness: Yes, when the heuristic is admissible
• Optimality: Yes, when the heuristic is admissible

Evaluation function

Recall that the Uninformed Cost Search (UCS) minimises the cost so far ($g(n)$), greedy search minimises the estimated cost to the goal ($h(n)$). A* combines UCS and greedy search. Its evaluation function is given below: $f(n)=g(n)+h(n)$ Where:

• $g(n)$ = cost so far to reach $n$
• $h(n)$ = estimated cost from $n$ to the goal
• $f(n)$ = estimated total cost of path through $n$ to the goal

Pseudocode

Similar to UCS, A-start uses a priority queue that ranks nodes in terms of their value calculated by the evaluation function.

A_Star(Graph, start, goal):
    1. Create a priority queue (PQ) and insert (start, f(start))
    2. Create a dictionary g_score to store the cost from start to each node (initialize with infinity)
    3. Set g_score[start] = 0
    4. Create a dictionary came_from to store the parent of each node
    5. While PQ is not empty:
        a. Dequeue the node with the lowest f(n) value (current)
        b. If current == goal, reconstruct and return the path
        c. For each neighbor of current:
            i. Compute tentative_g_score = g_score[current] + edge cost
            ii. If tentative_g_score < g_score[neighbor]:
                - Update g_score[neighbor]
                - Update f(neighbor) = tentative_g_score + h(neighbor)
                - Add (neighbor, f(neighbor)) to PQ
                - Update came_from[neighbor] = current
    6. If goal is not found, return failure

Admissible heuristic

If the heuristic $h$ is an admissible heuristic, then A* is complete and optimal. The heuristic $h$ is admissible if and only if $h$ never overestimates the true cost to the goal.

Let’s define:

• $s$: a state
• $S$: All possible states

$h(s)=\text{heuristic estimate from s to the goal}$ $c(s)=\text{optimal cost from s to the goal}$

$h$ is admissible if and only if: $\text{for all }s\in S:h(s)\le c(s)$

Consistent (monotone) heuristic

A consistent heuristic implies admissibility.

Definition

A heuristic function $h(n)$ is consistent if, for every state (node) $s$ and its successor (neighbours) $n$ (with step cost $c(s,n)$): $h(n)\le c(s,n)+h(n)$ Convert them into full mathematical notation:

$$\begin{array}{c}h(n)\le c(s,n)+h(n)\\ \\ \text{for all }s\in S\text{ and all }n\in \text{neighbours}(s)\\ c(s,n)=\text{step cost from s to n}\\ neighbours(s)=\text{set of all state s one step from s}\end{array}$$

The term $c(s,n)$ is the cost from $s$ to any its neighbour.

Intuition (triangle inequality)

Remember that the $h(n)$ is the estimated cost from $n$ to the goal node, and the definition of a consistent $h(n)$ defines that the estimated cost from $n$ to the gaol should never be greater than the actual cost to a successor + the estimated cost from that successor to the goal.

The triangle inequality

The triangle inequality is a fundamental concept in mathematics (geometry), stating that:

For any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side.

In mathematical notation: In a triangle, $c\le a+b$ Where $a,b,c$ are sides of the triangle.

Link to consistent heuristic

In the below diagram, we have these elements that form a triangle:

• A node $n$
• The estimated cost from $n$ to the goal $h(n)$
• A neighbour of $n$: $s$
• The estimated cost from $s$ to the goal $h(s)$

The dashed-line edges and nodes contribute to whatever paths between the $n$ and the goal and the $s$ and the goal. 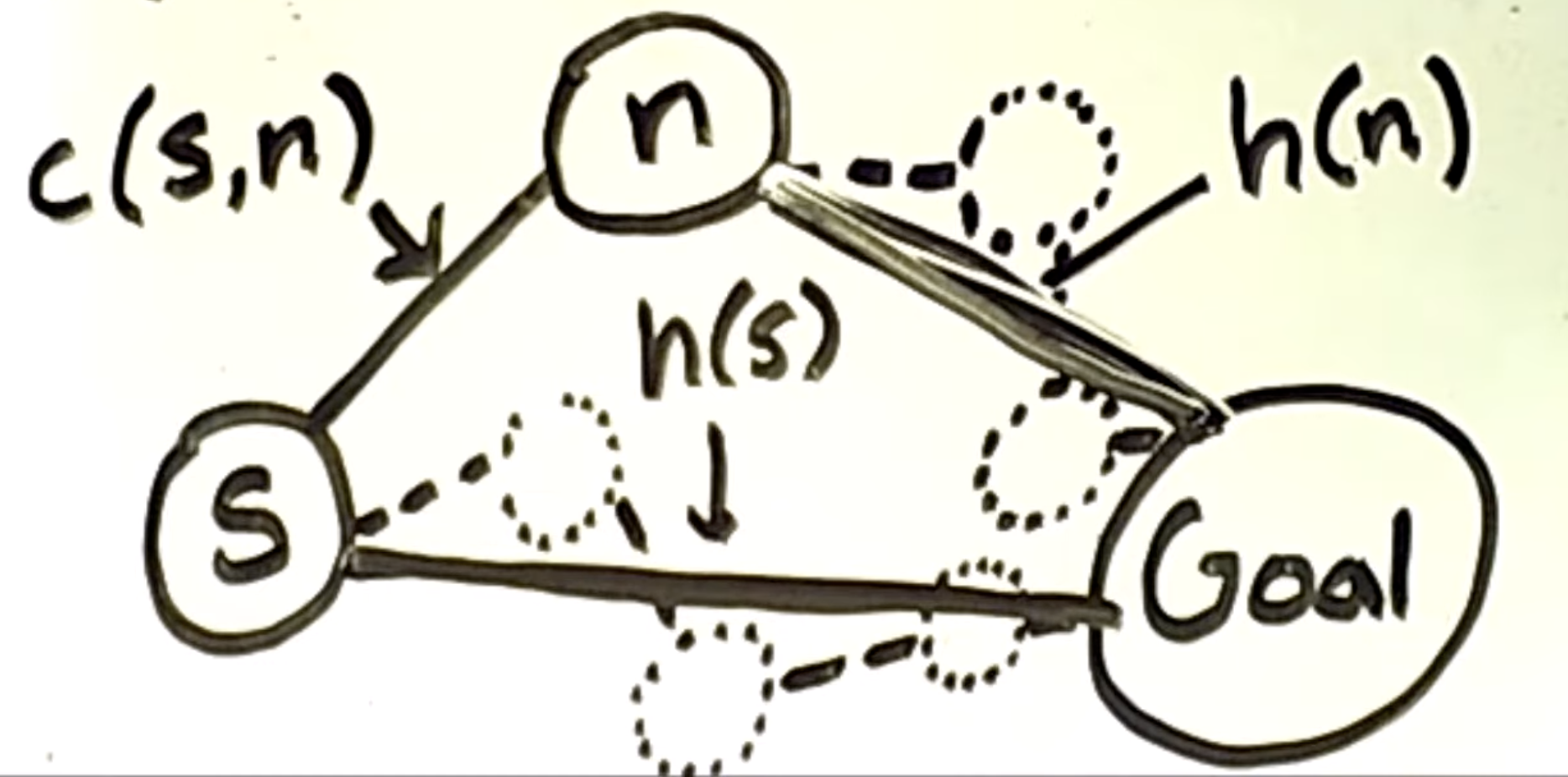To obey the triangle inequality rule, $h(s)$ has to be less than or equal to $c(s,n)+h(n)$. This means when moving from $n$ to $s$, the heuristic estimate $h(n)$ cannot decrease by more than the actual step cost $c(s,n)$. The consistency condition ensures that the heuristic estimate at node $n$ is never over-optimistic.

Consequence of consistent heuristic

When a heuristic is consistent, A* search never needs to revisit a node with a lower cost, meaning that the first time A* visits a node, it is guaranteed to be on the optimal path.

Any heuristic that is consistent, implies its admissibility. In another word, if a heuristic $h(n)$ is consistent, then it is also admissible (i.e. it never overestimates the true cost to the goal).

Search efficiency

The admissibility guarantees A* finds the optimal path, but it does not suggest the search is efficient (how fast it finds that path). If $h(n)$ is very small or zero, A* behaves like UCS. Consider the below scenario:

• $\text{for all }s\in S:c(s)\ge 0$
• $\text{for all }s\in S:h(s)=0$

$g(s)=\text{cost from start to s}$

The heuristic priority of $s$ is:

$$\begin{array}{rl}s& =g(s)+h(s)\\ & =g(s)+0\\ & =g(s)\end{array}$$

Which is equivalent to UCS that accumulates the cost to current node.

Therefore, we want the heuristic to be as large as possible but still being admissible.

Summary

• If $h(n)$ is admissible, A* is optimal

• If $h(n)$ is consistent, A* is optimally efficient

• Admissible does not imply consistent

• Consistent implies admissible

If we can’t design an accurate admissible or consistent heuristic, it may be better to settle for a non-admissible heuristic that works well in practice or for a local search algorithm even though completeness and optimality are no longer guaranteed. Also, although dominant (i.e. good) heuristics are better, they may need a lot of time to compute (time and space complexity are exponential); it may be better to use a simpler heuristic - more nodes will be expanded but overall the search may be faster.

When A-star behaves like BFS?

Breadth-First Search (BFS) searches node level by level and does not use heuristic information. If we set: $f(n)=\text{depth}(n)$ This can be think of: $g(n)=\text{depth}(n),h(n)=0$

Since $g(n)$ is the depth of the node, A* expands nodes purely based on their depth and will not go deeper (since they have greater depth value) unless the current depth is fully expanded.

---

Back to parent page: Problem Solving and Search

AI AI_Algorithm Problem_Solving Informed_Search A-Start_Search