Game Playing

Game playing in AI refers to the use of artificial intelligence techniques to develop agents that can play and compete in games. For this chapter, an understanding in Problem Solving and Search and related algorithms is needed.

Characteristics of games

• Deterministic VS chance
  • Deterministic: The game’s outcome is completely determined by player’s action, with no randomness involved
  • Chance-based: The game includes elements of randomness, such as dice rolls or shuffled cards
• Perfect VS imperfect information
  • Perfect information: Every player has complete knowledge of the game state at all times
  • Imperfect information: Some aspects of the game state are hidden from certain players (e.g. Poker, the player can’t see opponents’ hands)
• Zero-sum VS non-zero-sum
  • Zero-sum: One player’s gain is another player’s loss. The total value remains constant
  • Non-zero-sum: Players can cooperate, and the total payoff can vary. One player’s gain doesn’t necessarily mean another player’s loses

Example game playing

Specific setting

• 2 players - MAX and MIN
• Players take turns
• No chance involved (e.g. no dice)
• Perfect information game
• Zero-sum game

Examples: chess, tic-tac-toe

Possible way to play

• Consider all legal moves you can make from the current position
• Compute all new positions resulting from these moves
• Evaluate each new position and determine the best move
• Make that move
• Wait for your opponent to move and then repeat

Game playing as search

• State
  • Board configuration
• Initial state
  • The board configuration at the start. It includes which player’s turn it is
• Terminal states
  • Board configurations where the game is over
• Operators
  • Legal moves a player can make
• Utility function
  • A function that assigns a numerical value to terminal states
  • For example:
    • MAX wins → +1
    • MIN wins → -1
    • Draw +0
  • The higher the value, the better outcome for MAX
• Evaluation function
  • Numeric value associated with non-terminal states, shows how good the state is. (e.g. how close it is to a win)
• Game tree
  • Represents all possible game scenarios

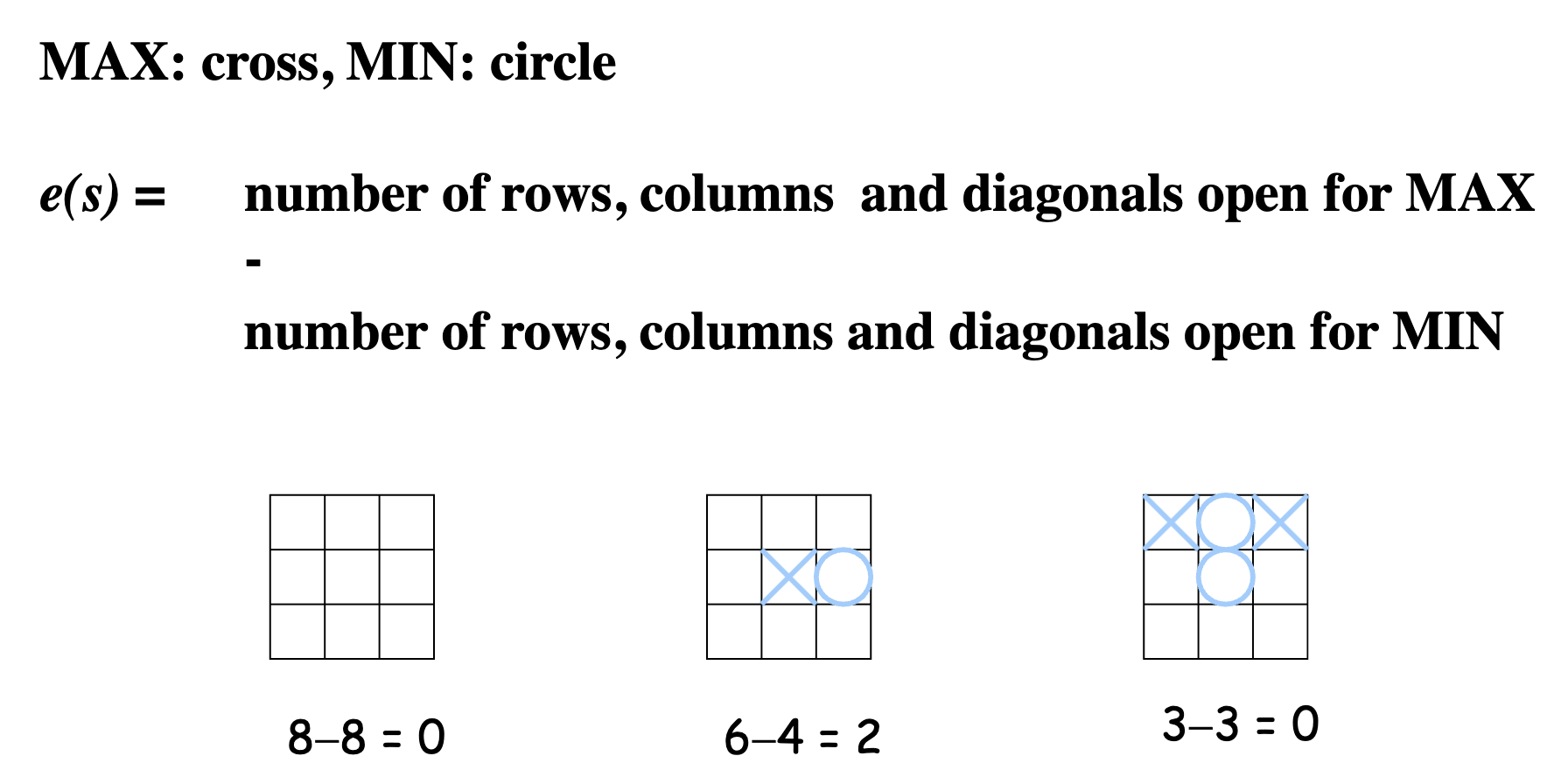
Evaluation function

A numeric value $e(s)$ associated with each non-terminal state $s$. Similar to heuristic functions in informed search problems. It gives the expected outcome of the game from the current position, for a given player (e.g. MAX).

Value $e(s)$ :

• Is a heuristic value that estimates how favourable $s$ is for MAX
• $e(s)$ > 0: $s$ is favourable for MAX
• $e(s)$ < 0: $s$ is favourable for MIN
• $e(s)=0$: $s$ is neutral

The higher the value e(s), the more favourable the position s is for MAX.

Consider the tic-tac-toe example below:

Game playing algorithms

• Minimax Algorithm

---

Back to parent page: Computational Data Science and Artificial Intelligence (AI)

AI AI_Algorithm Game_Playing