Binary Search

Related paradigm:

• Divide and Conquer

AlgorithmDivide_and_ConquerBinary_Search

---

Binary search algorithm is an efficient algorithm using the divide and conquer paradigm. The input to a binary search algorithm is an ordered data, the algorithm reduces the search range by half in each round until the target element is found or the search interval is empty.

• Input
  • an ordered array
  • a target number
• Output
  • the index of the target number

Example

• Input
  • {1, 3, 5, 6, 9, 12}, 9
• Output
  • 4

Implementation (Array)

// returns the index of the target 
private static int binarySearch(int[] nums, int target) {  
    int n = nums.length;  
    return binarySearchHelper(nums, target, 0, n-1);  
}  
  
private static int binarySearchHelper(int[] nums, int target, int left, int right) {  
    if (left > right) return -1;  
		int mid = left + (right - left) / 2; //prevent over flow
    if (nums[mid] > target) {  
        return binarySearchHelper(nums, target, left, mid - 1);  
    } else if (nums[mid] < target) {  
        return binarySearchHelper(nums, target, mid+1, right);  
    }  
    return mid;  
}

Here the mid is not calculated using traditional (left+right)/2 as this expression may cause integer overflow when left and right are both large integers:

int a = Integer.MAX_VALUE - 10; 
int b = Integer.MAX_VALUE;
int glitchyAdd = a + b; 

Calculate the mid point using left+(right-left)/2; can mitigate this issue.

Correctness proof

Invariant: If x is in nums before the divide step, then x is in nums after the divide step.

• If nums[n/2] > x, then x must be in nums[0 to [n/2]-1]
• if nums[n/2] < x, then x must be in nums[[n/2]+1 to n-1]

Every divide step leads to a smaller array. Thus, if x in nums, we will eventually inspect its position due to the invariant and return “Found”. Thus, if x is not in nums, then eventually we reach the empty array and return “Not Found”.

Time complexity (Array)

The time complexity of the algorithm is proved with the recurrence formula.

In array binary search:

• Divide: find the middle and compare to x takes $O(1)$
• Recur: solve the left or right subproblem takes $T(n/2)$
• Conquer: return the answer from recursion takes $O(1)$

The time complexity in general form can be described as: $T(n)=\{\begin{array}{ll}\text{T(n/2) + O(1)}& \text{for }n>1\\ \text{O(1)}& \text{for }n=1\end{array}$

Proof by unrolling

The below diagram shows the recursion process unrolled, breaking down the function calls until it reaches the base case (subproblem of size 1).

• The zero level from top represents the time complexity to search an array of size $n$, $c$ is the time it takes to perform comparison and other basic operation, in binary search, the operations are in dependent of the input size, therefore they are in constant time.
• The first level represents the time to search a sub-array of size $n/2$.
• The second level represents the the time to search a sub-array of size $n/4$, and so on.
• The $k$ level represents the time to search a sub-array of size $n/2^k$, where $k$ is the level of recursion. For example, when $k=2$, the size of the sub-array is $n/2^2=n/4$.

The depth of the recursion tree is $\log n$ because each recursive call halves the problem size until it reaches the base case.

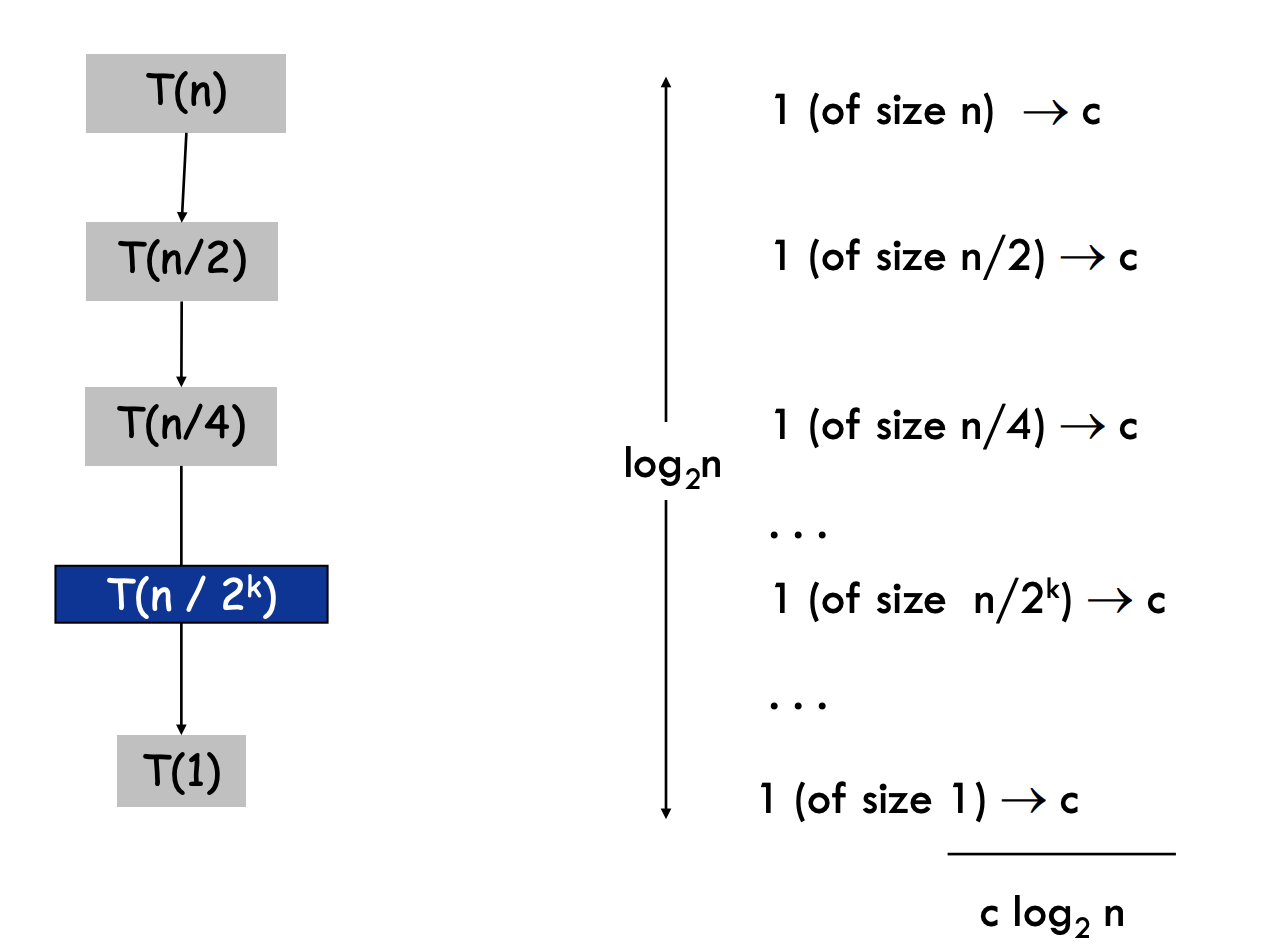
Summing the cost

The total time complexity is the sum of the costs at each level. In this case, each recursion level takes constant time $c$ to solve, the depth of recursion is $\log n$, therefore the total time cost is $c\times \log n=c\log n$

Time complexity (Linked list)

In array binary search:

• Divide: find the middle and compare to x takes $O(n)$, to get an element in linked list takes linear time
• Recur: solve the left or right subproblem takes $T(n/2)$
• Conquer: return the answer from recursion takes $O(1)$

The time complexity in general form can be described as: $T(n)=\{\begin{array}{ll}\text{T(n/2) + O(n)}& \text{for }n>1\\ \text{O(1)}& \text{for }n=1\end{array}$

Proof by unrolling

Similar to the array binary search, but this time the comparison takes $O(n)$ time, since retrieve the value of an element takes linear time. Therefore, combine with other basic operations $c$, the recur step takes $c\times O(n)$ time.

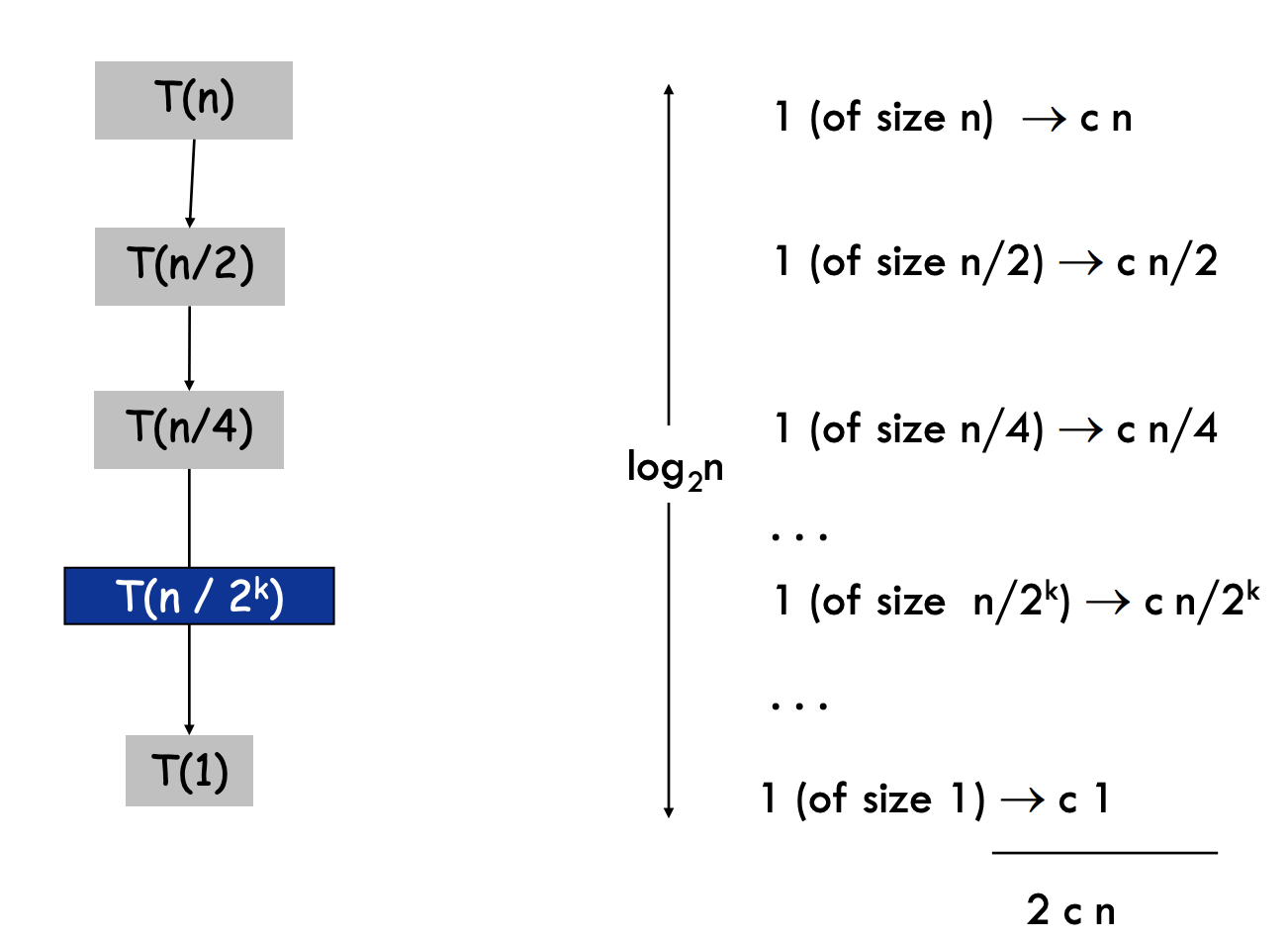
Summing the cost

The total time complexity is the number of recursion levels multiplied by the time cost in each recursive call, which can be described as:

$$\begin{array}{rl}\text{Time Complexity}& =\log n\times (c\cdot n+c(n/2)+c(n/4)+...c(n/2^k)...+c\cdot 1)\\ & =\log n\times (c\times (n+n/2+n/4+...+1))\\ & =\log n\times (c\times (\frac{n}{1/2}))\\ & =\log n\times (c\times 2n)\\ & =\log n\times 2cn\\ & =2cn\end{array}$$

The evaluation employs the geometric series rule.

---

Back to parent page: