Abstract data type:

ADT - Tree
- ADT - Binary Tree

Implementation:

In computer science, a tree is an abstract model of a hierarchical structure. A tree T consists of nodes (vertices) with a parent-child relation.

If T is non-empty, it has a special node called the root that has no parents.
Every node v of T other than the root has a unique parent.
Following the parent relation always lead to the root.

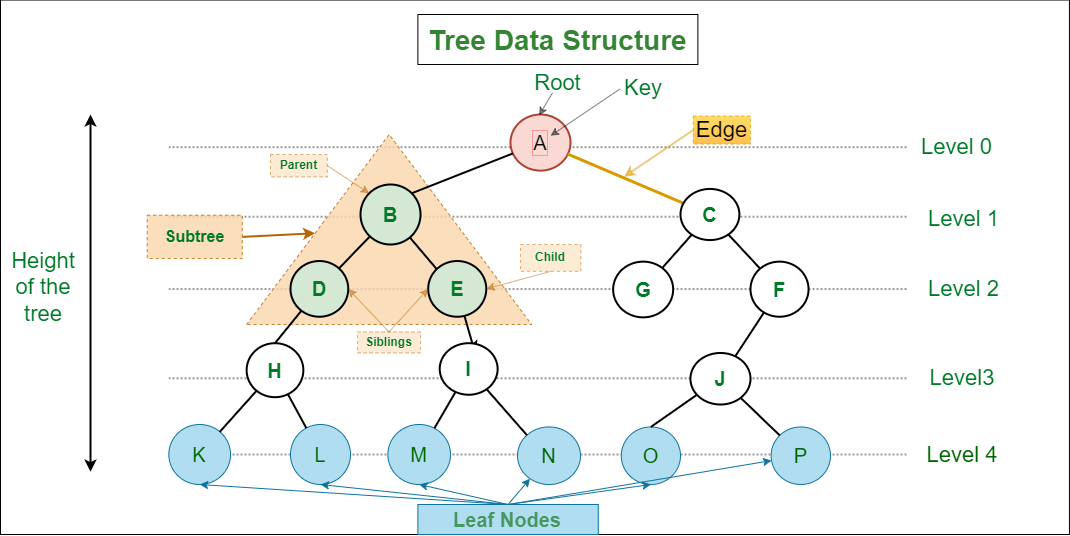
Tree terminology

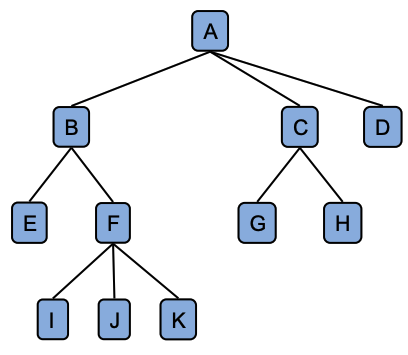
Node classification

Root
- Node without parent (A)
Internal node
- Node with at least one child (A, B, C, F)
External/leaf node
- Node without children (E, I, J, K, G, H, D)

Node relations

Ancestors
- Parent, grandparent, great-grandparent, etc. (e.g. ancestors of F are A and B)
Descendants
- Child, grandchild, great-grandchild, etc. (e.g. descendants of B are E, F, I , J, K)
Siblings
- Two nodes with the same parent are siblings (B, D)

Location concepts

Depth of a node
- Number of edges present in path from the root node to that node (e.g. depth(F) = 2)
Level
- Set of nodes with given depth, level starts from 0 (e.g. {E, F, G, H} are level 2)
Height of a tree
- maximum depth, or the number of edges from the leaf node to a particular node in the longest path. (e.g. the height of node B is 2)

Substructure of a tree

Subtree
- A smaller tree that is entirely contained within a larger tree, containing a node and all of its child nodes, grandchild nodes, and so on
Edge
- A connection or link between two nodes
Path
- A sequence of connected nodes and edges in a graph or tree, representing a route that can be traversed

Operations

Position as node abstraction
Generic methods
- integer size()
- boolean isEmpty()
- Iterator iterator()
- Iterable positions()
Access methods
- Position root()
- Position parent(p)
- Iterable children(p)
- Integer numChildren(p)
Query methods
- boolean isInternal(p)
- boolean isExternal(p)
- boolean isRoot(p)

Node ADT

value: the value associated with this node
children: set or list of children of this node
parent(optional): the parent of this node

Traversing trees

A traversal visits the nodes of a tree in a systematic manner.

pre-order (on the left)
post-order (on the right)
in-order (from below)

Preorder traversal

For preorder traversal we print a node when we pass to its left in the cycle 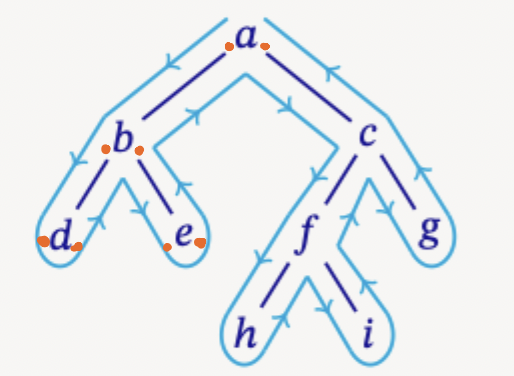The preorder traversal sequence will be: a, b, d, e, c, f, h, i, g

void preorderTraversal(TreeNode root) {
	if (node != null) {
		System.out.println(root.value);
		traversePreorder(root.left);
		traversePreorder(root.right);
	}
}

Postorder traversal

For preorder traversal we print a node when we pass to its right in the cycle The postorder traversal sequence will be: d, e, b, h, i, f, g, c, a

void postOrderTraversal(TreeNode root) {
	if (node != null) {
		traversePreorder(root.left);
		traversePreorder(root.right);
		System.out.println(root.value);
	}
}

Inorder traversal

For in-order traversal we print a node when we pass to its bottom in the cycle. The in-order traversal sequence will be: d, b, e, a, h, f, i, c, g

void traverseInorder(TreeNode root) {
	if (root != null) {
		traverseInorder(root.left);
		System.out.println(root.value)
		traverseInorder(root.right);
	}
}

Level order traversal

Level order traversal or sometimes known as breadth-first traversal, visits nodes level by level from left to right. The level-order traversal sequence will be: a, b, c, d, e, f, g, i

List<Integer> levelOrderTravesal(TreeNode root) {
	List<Integer> results = new ArrayList<>();
	if (root == null) {
		return result;
	}
	Queue<TreeNode> queue = new LinkedList<>();
	queue.add(root);
	
	while(!queue.isEmpty()) {
		TreeNode currentNode = queue.poll();
		result.add(currentNode.value);
		if (currentNode.left != null) {
			queue.add(currentNode.left);
		}
		if (currentNode.right != null) {
			queue.add(currentNode.right);
		}
	}
	return result;
}

Back to parent node: Data Structures and Algorithms

Computer Science Wiki

Explorer

ADT - Tree