Hill-Climbing Search

Hill climbing search algorithm is a heuristic search algorithm which continuously moves in the direction of increasing value to find the peak of the mountain or best solution to the problem. It keeps track of one current state and on each iteration moves to the neighbouring state with the highest value.

Variations

• Steepest ascent - the goal is the maximum value
• Steepest descent - the goal is the minimum value

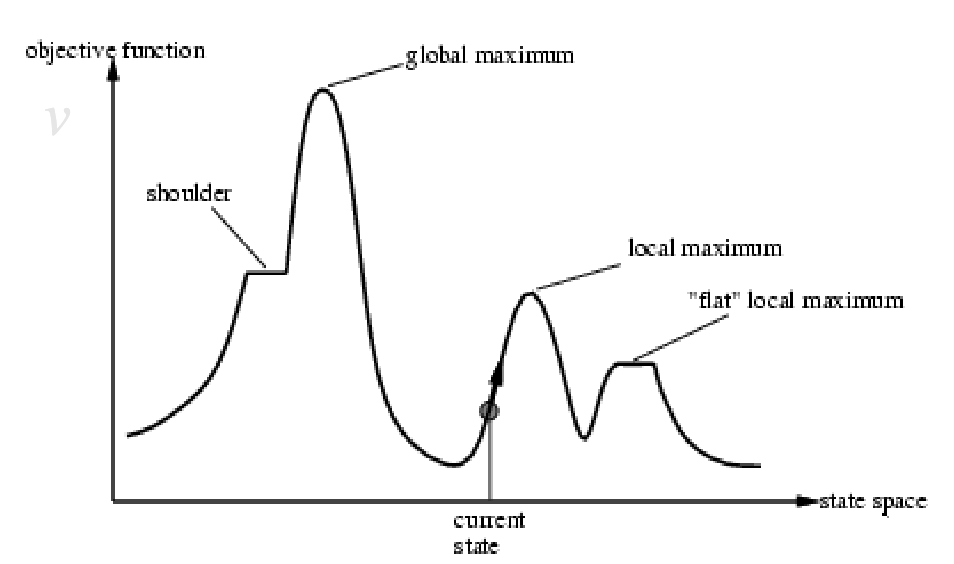
The algorithm can’t see the whole landscape, only the neighbouring states. It keeps only 1 state in memory, no back tracking to previous states (Local search algorithms).

Pros and cons

• Cons
  • Can easily get stuck in a local optimum
  • However, not all local optimum are bad, some are good enough even though not optimal
• Pros
  • Good choice for hard, practical problems
  • Uses very little memory
  • Finds reasonable solution in large spaces where systematic algorithms are not useful

V-value

Each state has a value $v$ that we can compute.

Escaping bad local optima

Hill climbing finds the closest local optimum (minimum or maximum, depending on the version - descent or ascent), which may not be the global optimum. The solution that is found depends on the initial state (its displacement within the state space)

Pseudocode

This is a descent version.

HillClimbing(problem):
    1. Set current ← initial_state(problem)
    2. While True:
        a. Generate neighbors of current
        b. Select the neighbour based on objective function
        c. If best neighbor is better than current:
            i. Set current ← best neighbor
        d. Else:
            i. Return current (local optimum found)