Uninformed Search - Iterative Deepening Search (IDS)

Iterative Deepening Search (IDS) combines the space efficiency and optimality of Breadth-First Search(BFS) when all step costs are equal. Instead of diving deep immediately like Depth-First Search (DFS), IDS repeatedly runs a Depth-Limited Search (DLS) with increasing depth limit until the goal is found.

• Completeness: Yes, as BFS
• Optimality: Yes, as BFS

Depth-Limited Search (DLS)

Depth-Limited Search (DLS) is a modified version of DFS. It stops at a predefined depth instead of exploring indefinitely. IDS runs a DFS up to a certain depth limit to prevent infinite loops in deep graphs.

Pseudocode

IterativeDeepeningSearch(Graph, start, goal):
    1. Set depth = 0
    2. While True:
        a. result = DepthLimitedSearch(Graph, start, goal, depth)
        b. If result is not "cutoff", return result (goal found or failure)
        c. Increase depth and repeat

DepthLimitedSearch(Graph, current, goal, depth_limit):
    1. If current is the goal, return the path
    2. If depth_limit == 0, return "cutoff" (stop exploring deeper)
    3. For each neighbor of current:
        a. result = DepthLimitedSearch(Graph, neighbor, goal, depth_limit - 1)
        b. If result is not "cutoff", return result (goal found or failure)
    4. Return "cutoff" if no solution is found within depth_limit

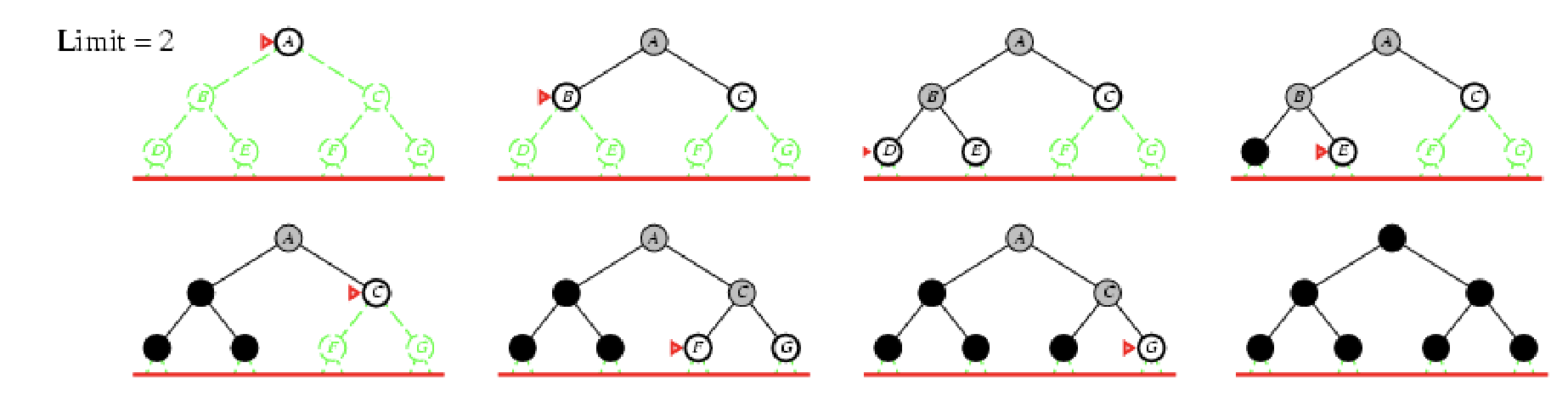
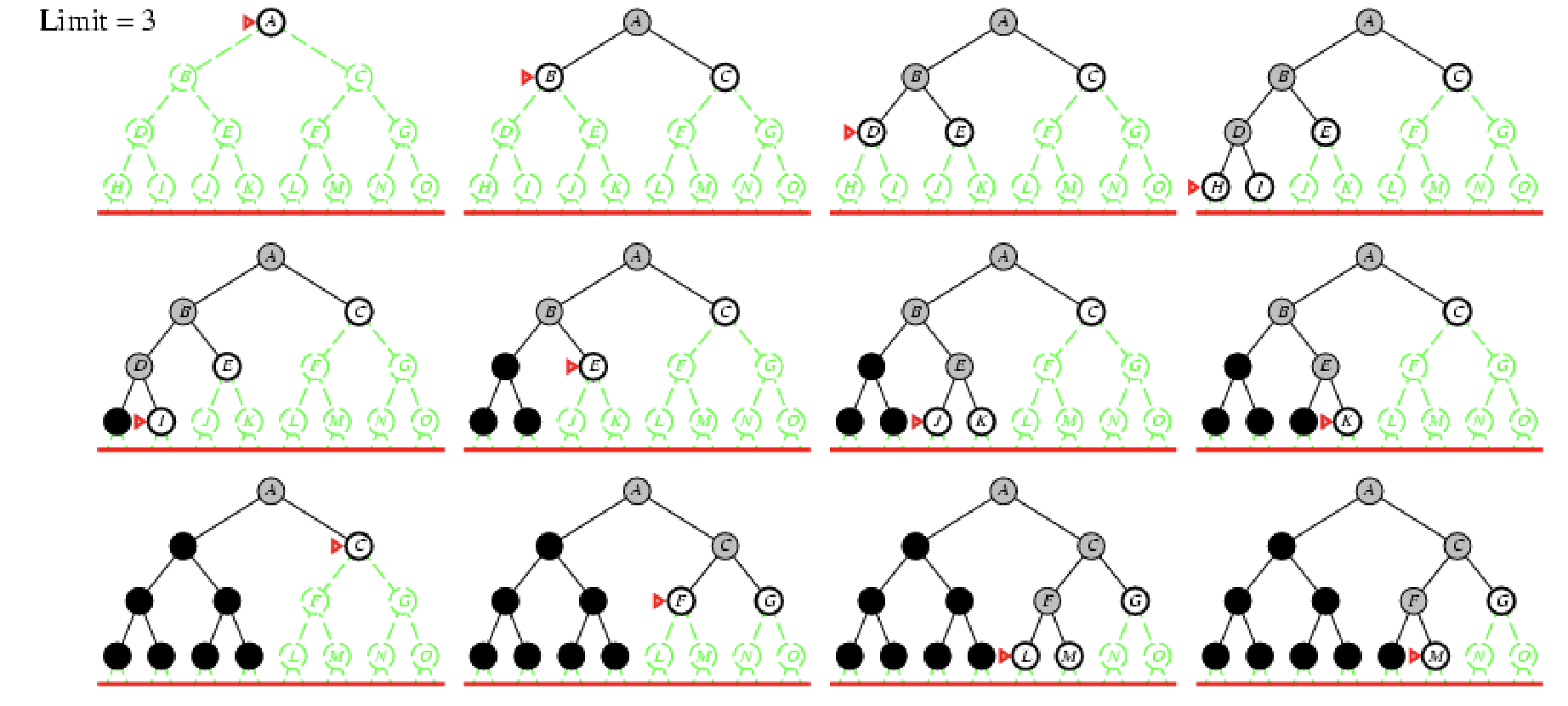
Example

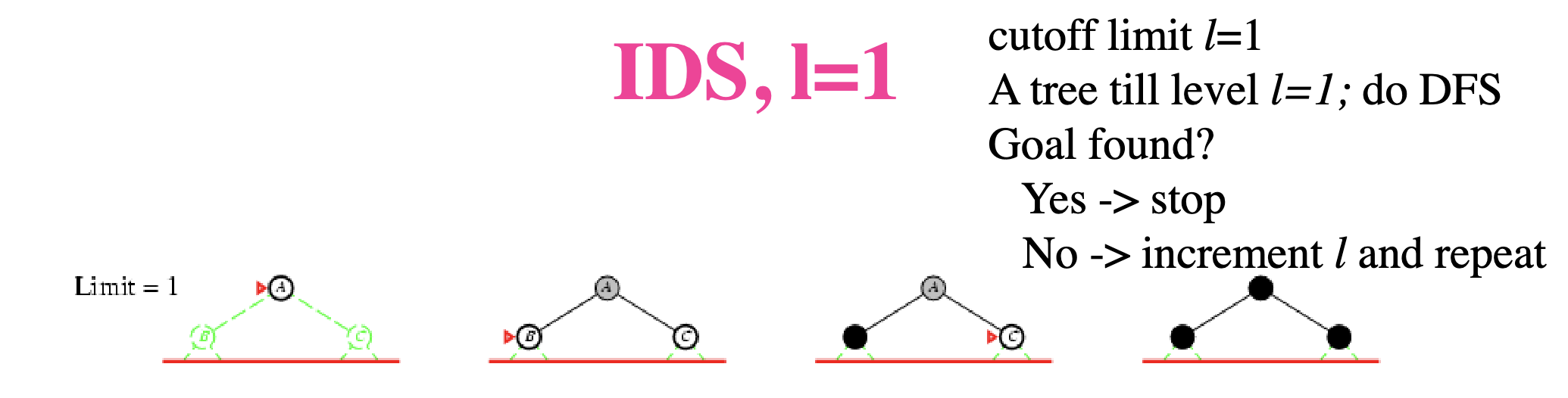
l=2

l=3

Multiple expansion overhead

IDS repeatedly expands the same nodes in earlier depth-limited search before reaching the goal. This happens because IDS restarts from the root node at every depth limit, leading to redundant computations.

Overhead is small for most problems

Even though IDS expands nodes multiple times, the overhead remains small for most practical problems. This is mainly because of the geometric growth of nodes per level in a tree.

In a tree problem, the majority of nodes are at the deepest level of the tree. The number of nodes grow exponentially with depth. Earlier levels have very few nodes, so their repeated expansion doesn’t contribute much to the total cost.

Consider this example:

• Branching factor (b) = 10 (each node has 10 children)
• Depth limit (d) = 5 (goal is found at depth 5)

Depth	Nodes at this level	Total Nodes (BFS)	Cumulative Nodes Expanded (IDS)
0	1	1	1
1	10	11	12
2	100	111	123
3	1,000	1,111	1,234
4	10,000	11,111	12,345
5	100,000	111,111	123,456
**Total nodes expanded by [[Graph Breadth-First Search (BFS)	BFS]]**
${\sum }_{i=0}^5{b}^i=1+10+100+1,000+10,000+100,000=111,111$

Total nodes expanded by IDS ${\sum }_{i=0}^5(d-i)\times b^i=123,456$ The final sum is about $1.1\times$ BFS.

Time complexity

As discussed above, the IDS can revisit previous nodes. The total number of node expansions is given by: ${\sum }_{i=0}^5(d-i)\times b^i$ Using the sum approximation: $O(\frac{b^d}{1-\frac{1}{b}})\approx O(b^d)$ Which is same as BFS but with a small constant overhead factor.

Space complexity

IDS behaves like DFS in terms of space. DFS only stores the current path (not the entire frontier like BFS). At depth d, the longest path stored in memory is d nodes. $O(bd)$

---

Back to parent page: Problem Solving and Search

AI AI_Algorithm Problem_Solving Uninformed_Search Iterative_Deepening_Search