Boundary Value Test

Boundary Value Testing is based on the idea that - Bugs are more likely to occur at the “boundaries” of input ranges than in the middle.

Boundary Value Weak test design uses the following inputs

• Minimum (min)
• Just above minimum (min+)
• A nominal value (nom, a typical or middle value within the valid range)
• Just below maximum (max-)
• Maximum (max)

Knowledge in Assumptions of Blackbox Testing is required.

Basic types of boundary value test

Equivalence partitioning can be applied with different assumptions based on whether fault interaction is expected and whether invalid inputs are possible.

	Normal	Robust
Weak	(best case)
Strong		(worst case)

• Weak Normal: Best case
  • Weak: No interactions between parameters
  • Normal: Only valid input values are considered, you are not dealing with complex invalid input
• Strong Robust: Worst case
  • Strong: Interactions between parameters
  • Robust: You have to consider invalid inputs

Single parameter weak normal boundary value

In this test case design, we assume:

• Weak: Each parameter is independent, only one input value causes bug at a time
• Normal: Only valid value is tested

Say we have a single parameter x1, which is valid in some range [a, b] . That is, a ≤ x1 ≤ b. 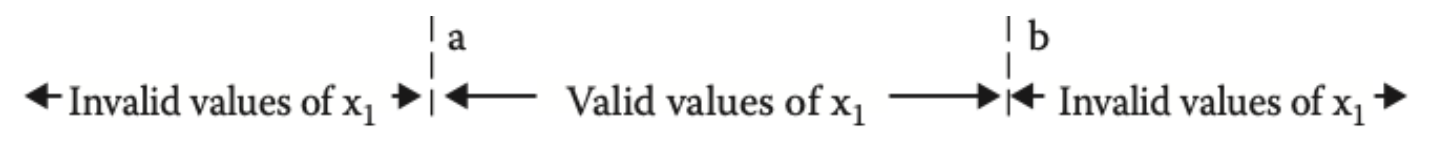So, we will have the following values for x1.

• min: a
• min+: a+1 (or with smallest delta, a + delta)
• nom: a < nom < b
• max-: b-1(or with smallest delta b - delta)
• max: b

For example:

a = 10
b = 20
So, valid range: 10 ≤ x1 ≤ 20

Test inputs to use:

Label	Value	Explanation
min	10	Lower boundary
min+	11	Just above lower boundary
nominal	15	A mid-range value (a < nom < b)
max-	19	Just below upper boundary
max	20	Upper boundary

Single parameter weak robust boundary value

In this test case design, we assume:

• Weak: Each parameter is independent, only one input value causes bug at a time
• Robust: Invalid value exists

In this case, invalid values are allowed, so we have to test values out of bound

• min-: a-1 (or with smallest delta, a - delta)
• min: a
• min+: a+1 (or with smallest delta, a + delta)
• nom: a < nom < b
• max-: b-1(or with smallest delta b - delta)
• max: b
• max+: b+1 (or with smallest delta b + delta)

Two parameter weak normal boundary value

In this test case design, we assume:

• Weak: Only one input causes a fault at a time, so we only vary one parameter at a time, and keep the other at a nominal value.
• Normal: All inputs are valid

Let’s say the function takes two inputs: x1 and x2, where:

• 10 ≤ x1 ≤ 20
• 100 ≤ x2 ≤ 200 We only vary one parameter at a time (test boundary value of each input independently), while holding the other input at its nominal (typical) value. We choose:
• For x1: min = 10, min+ = 11, nom = 15, max- = 19, max = 20
• For x2: min = 100, min+ = 101, nom = 150, max- = 199, max = 200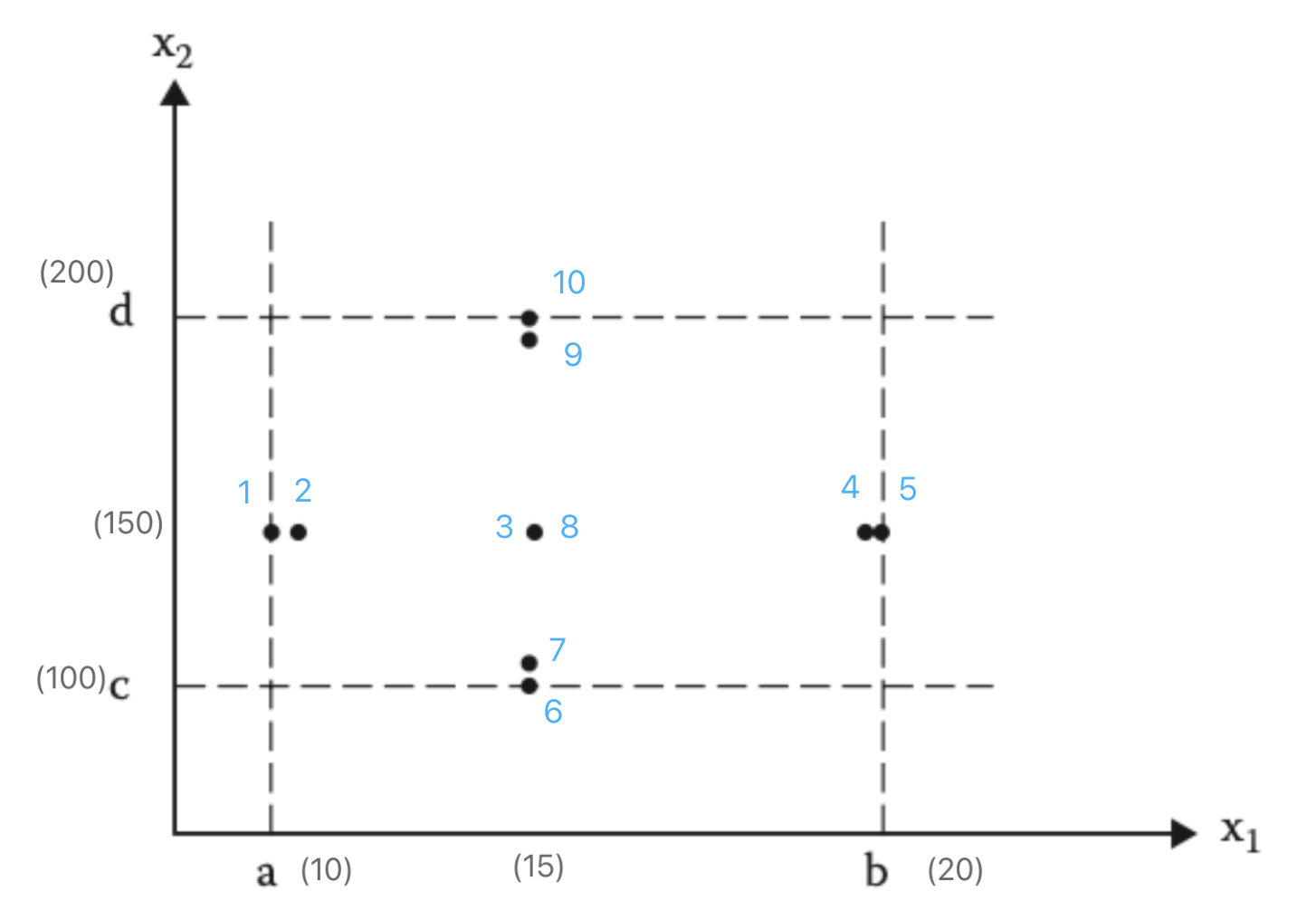 Step 1: Hold x2 at nominal (150), vary x1 across boundaries

Test	x1	x2	Notes
1	10	150	min
2	11	150	min+
3	15	150	nom
4	19	150	max-
5	20	150	max+
Step 2: Hold x1 at nominal (15), vary x2 across boundaries

Test	x1	x2	Notes
6	15	100	min
7	15	101	min+
8	15	150	nom
9	15	199	max-
10	15	200	max+

Two parameter weak robust boundary value

In this test case design, we assume:

• Weak: Only one input causes a fault at a time, so we only vary one parameter at a time, and keep the other at a nominal value.
• Robust: Invalid value exists, in addition to valid boundary values

Similar to previous test case design, let’s say the function takes two inputs: x1 and x2, where:

• 10 ≤ x1 ≤ 20
• 100 ≤ x2 ≤ 200

This time, we test both valid and invalid boundary values for each parameter individually, while keeping the other parameter at a valid nominal value. We choose:

• For x1: invalid below min = 9, min = 10, min+ = 11, nom = 15, max- = 19, max = 20, invalid above max = 21
• For x2: invalid below min = 99, min = 100, min+ = 101, nom = 150, max- = 199, max = 200, invalid above max = 201

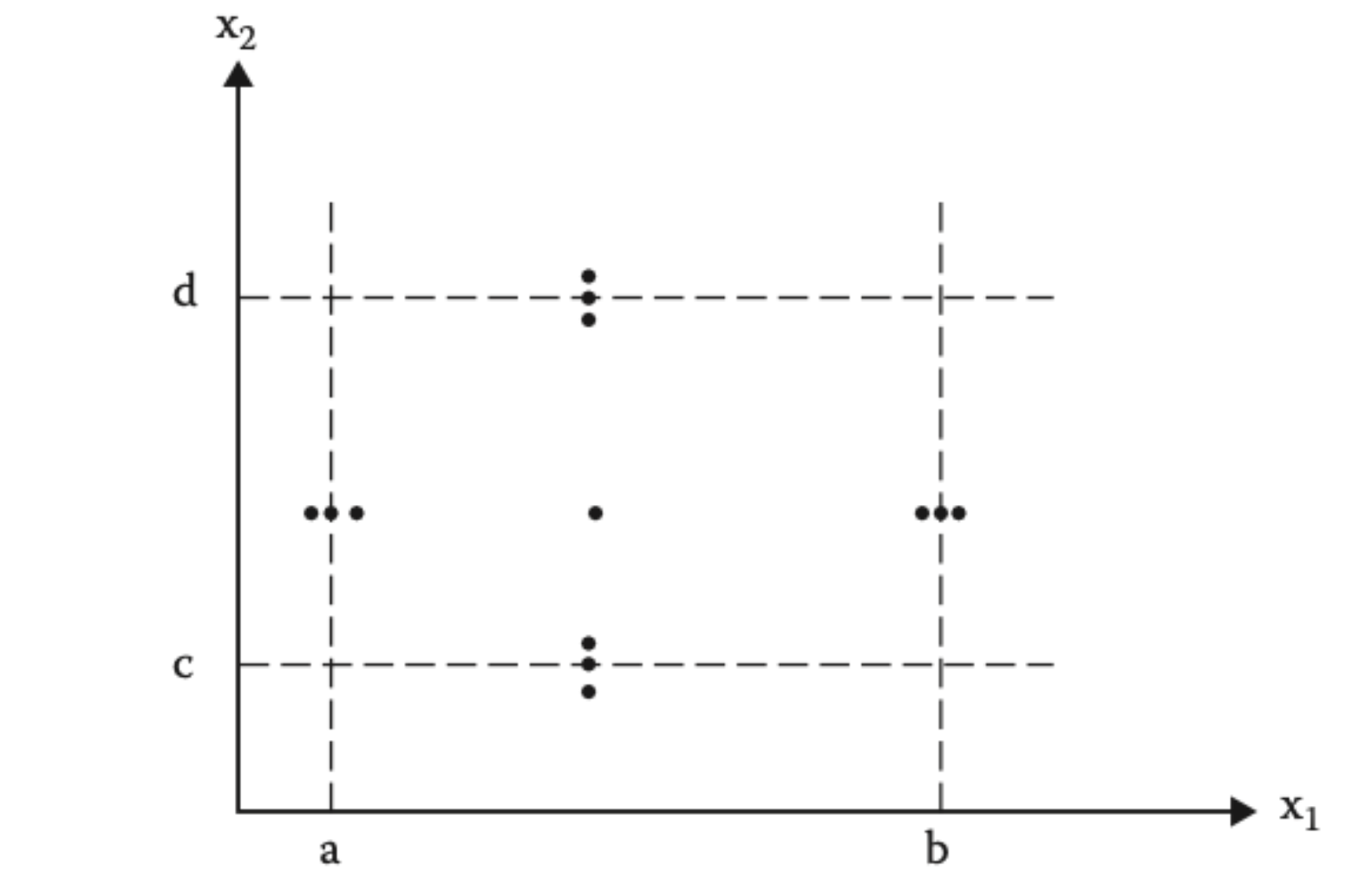
Step 1: Hold x2 at nominal (150), vary x1

Test	x1	x2	Notes
1	9	150	Invalid (below min)
2	10	150	Valid (min)
3	11	150	Valid (min+)
4	15	150	Valid (nom)
5	19	150	Valid (max-)
6	20	150	Valid (max)
7	21	150	Invalid (above max)
Step 2: Hold x1 at nominal (15), vary x2

Test	x1	x2	Notes
8	15	99	Invalid (below min)
9	15	100	Valid (min)
10	15	101	Valid (min+)
11	15	150	Valid (nom)
12	15	199	Valid (max-)
13	15	200	Valid (max)
14	15	201	Invalid (above max)

Two parameter strong normal boundary value

• Strong: All combinations of boundary values are tested together. That means we vary both parameters simultaneously at their boundary value.
• Normal: Only valid values are used (no invalid inputs).

Input ranges:

• x1: 10 ≤ x1 ≤ 20
• x2: 100 ≤ x2 ≤ 200

We use only valid boundary values for both parameters:

• For x1: min = 10, min+ = 11, nom = 15, max- = 19, max = 20
• For x2: min = 100, min+ = 101, nom = 150, max- = 199, max = 200

We then test all combinations of the boundary values of x1 and x2 together.

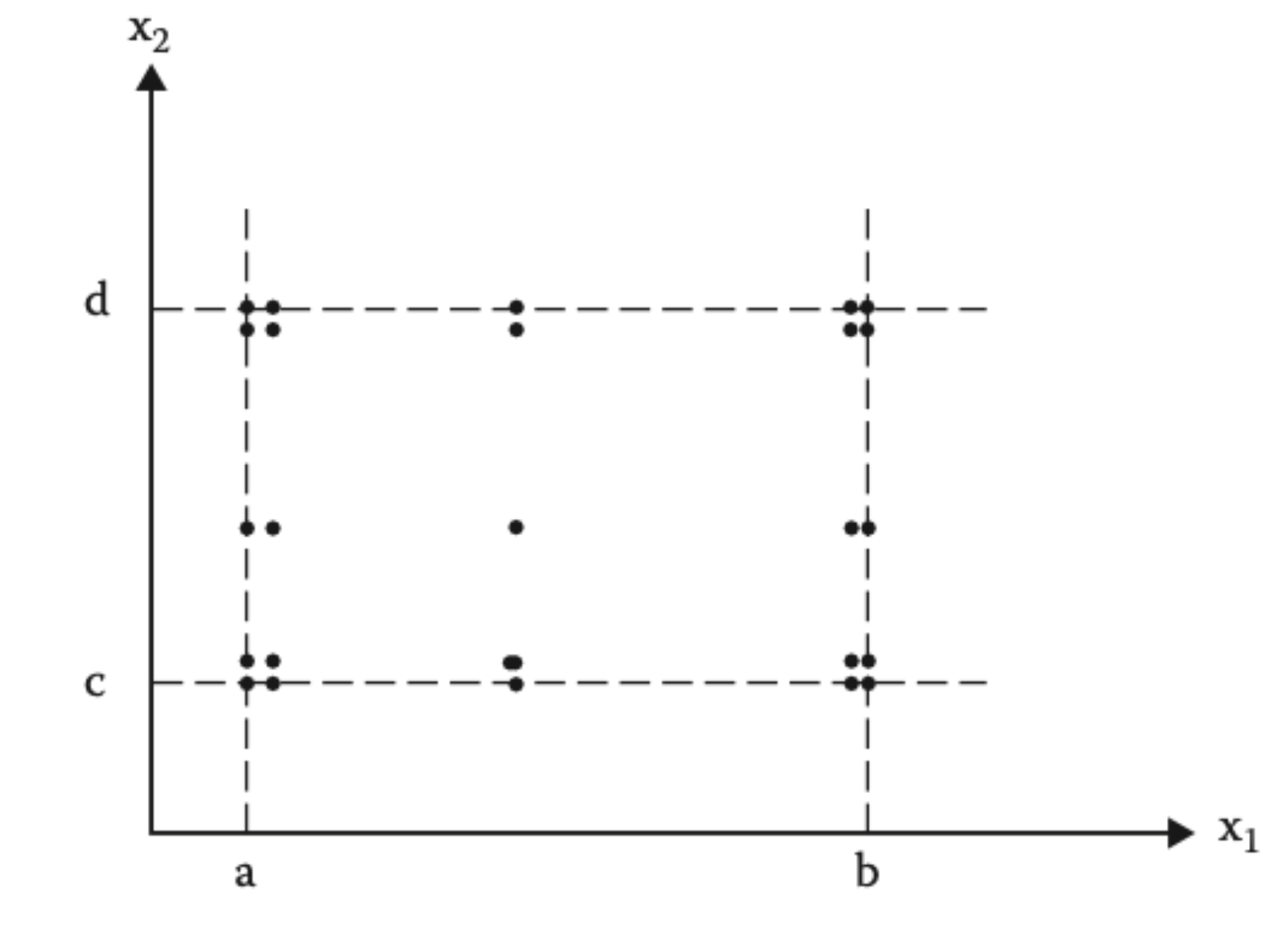
Test	x1	x2	Notes
1	10	100	Both at minimum
2	10	101	x1 at min, x2 at min+
3	10	150	x1 at min, x2 at nom
4	10	199	x1 at min, x2 at max-
5	10	200	x1 at min, x2 at max
6	11	100	x1 at min+, x2 at min
7	11	101	x1 at min+, x2 at min+
8	11	150	x1 at min+, x2 at nom
9	11	199	x1 at min+, x2 at max-
10	11	200	x1 at min+, x2 at max
11	15	100	x1 at nom, x2 at min
12	15	101	x1 at nom, x2 at min+
13	15	150	x1 and x2 both at nom
14	15	199	x1 at nom, x2 at max-
15	15	200	x1 at nom, x2 at max
16	19	100	x1 at max-, x2 at min
17	19	101	x1 at max-, x2 at min+
18	19	150	x1 at max-, x2 at nom
19	19	199	x1 at max-, x2 at max-
20	19	200	x1 at max-, x2 at max
21	20	100	x1 at max, x2 at min
22	20	101	x1 at max, x2 at min+
23	20	150	x1 at max, x2 at nom
24	20	199	x1 at max, x2 at max-
25	20	200	Both at maximum

Two parameter strong robust boundary value

• Strong: All combinations of boundary values are tested together. That means we vary both parameters simultaneously at their boundary value.
• Robust: Includes invalid values beyond the defined valid range.

Input Ranges:

• x1: 10 ≤ x1 ≤ 20

• x2: 100 ≤ x2 ≤ 200

• For x1: invalid below min = 9, min = 10, min+ = 11, nom = 15, max- = 19, max = 20, invalid above max = 21

• For x2: invalid below min = 99, min = 100, min+ = 101, nom = 150, max- = 199, max = 200, invalid above max = 201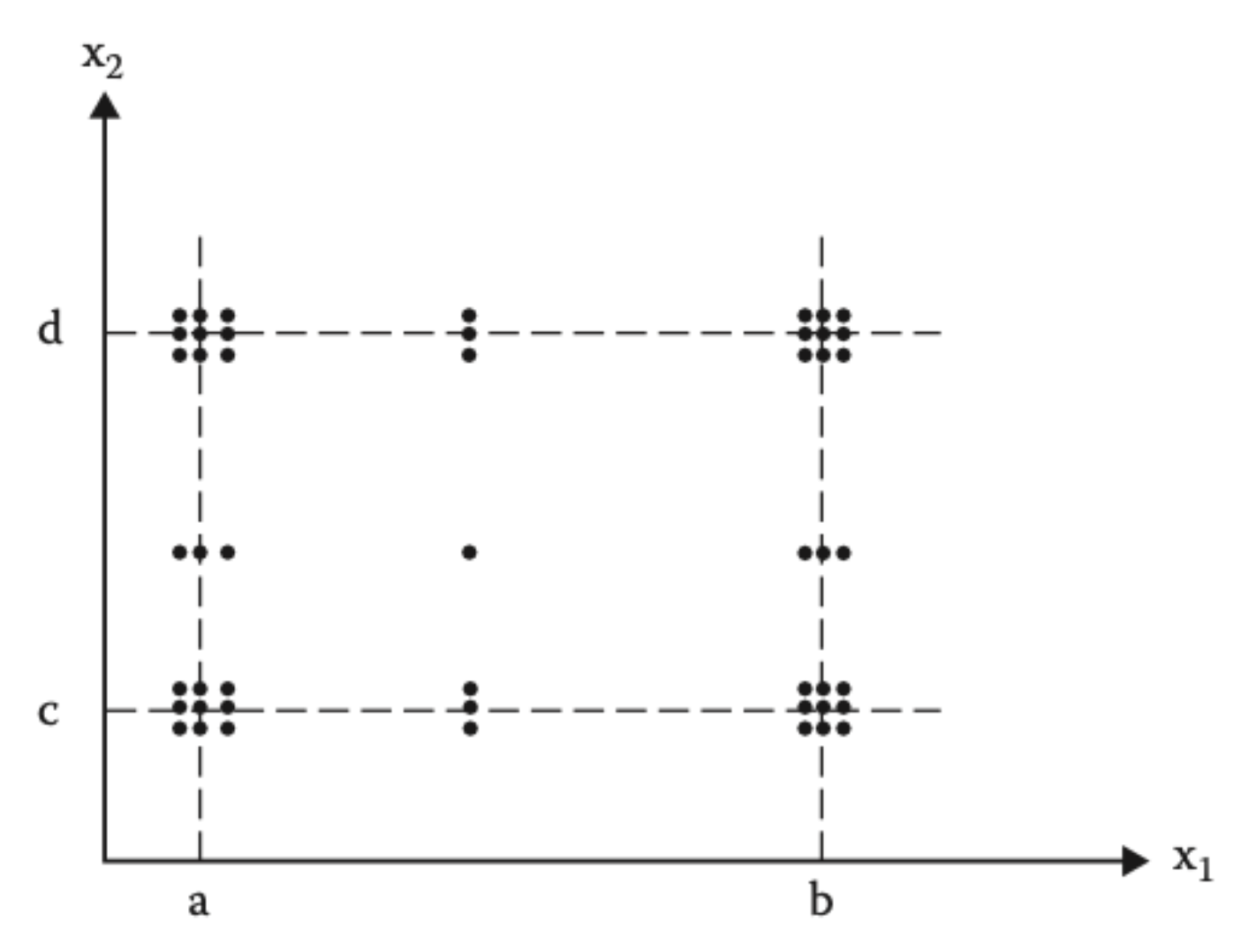

Test	x1	x2	Notes
1	9	99	Both invalid (below min)
2	9	100	x1 invalid, x2 at min
3	9	101	x1 invalid, x2 at min+
4	9	150	x1 invalid, x2 at nom
5	9	199	x1 invalid, x2 at max-
6	9	200	x1 invalid, x2 at max
7	9	201	x1 invalid, x2 invalid (above max)
8	10	99	x1 at min, x2 invalid
9	10	100	Both at min
10	10	101	x1 at min, x2 at min+
11	10	150	x1 at min, x2 at nom
12	10	199	x1 at min, x2 at max-
13	10	200	x1 at min, x2 at max
14	10	201	x1 at min, x2 invalid
15	11	99	x1 at min+, x2 invalid
16	11	100	x1 at min+, x2 at min
17	11	101	Both valid (min+, min+)
18	11	150	Valid (min+, nom)
19	11	199	Valid (min+, max-)
20	11	200	Valid (min+, max)
21	11	201	x1 valid, x2 invalid
22	15	99	x1 at nom, x2 invalid
23	15	100	x1 at nom, x2 at min
24	15	101	x1 at nom, x2 at min+
25	15	150	Both nominal
26	15	199	x1 nom, x2 at max-
27	15	200	x1 nom, x2 at max
28	15	201	x1 nom, x2 invalid
29	19	99	x1 at max-, x2 invalid
30	19	100	x1 at max-, x2 at min
31	19	101	Valid
32	19	150	Valid
33	19	199	Valid
34	19	200	Valid
35	19	201	x2 invalid
36	20	99	x1 at max, x2 invalid
37	20	100	x1 at max, x2 at min
38	20	101	Valid
39	20	150	Valid
40	20	199	Valid
41	20	200	Both at max
42	20	201	x1 valid, x2 invalid
43	21	99	x1 invalid, x2 invalid
44	21	100	x1 invalid, x2 at min
45	21	101	x1 invalid, x2 at min+
46	21	150	x1 invalid, x2 at nom
47	21	199	x1 invalid, x2 at max-
48	21	200	x1 invalid, x2 at max
49	21	201	Both invalid (above max)

---

Back to parent page: Software Testing

Web_and_App_Development Software_Testing Blackbox_Testing SOFT3202 Boundary_Value_Test_Design

Two way testing

If at most p parameters interact to cause a fault:

• Number of test cases needed = $\left(\genfrac{}{}{0ex}{}{n}{p}\right)\cdot k^p=\frac{n!}{p!(n-p)!}\cdot k^p$

Where:

• n = total parameters
• k = values per parameter
• p = number of interacting parameters you want to test