RSA Algorithm

RSA is a asymmetric key encryption algorithm developed in 1977 by Ron Rivest, Adi Shamir, and Len Adleman. The name RSA is taken from their surname initials. The RSA is still popular as of now (2024) and could be replaced by post-quantum encryption algorithms in the future with the emerging of quantum computing.

RSA key generation

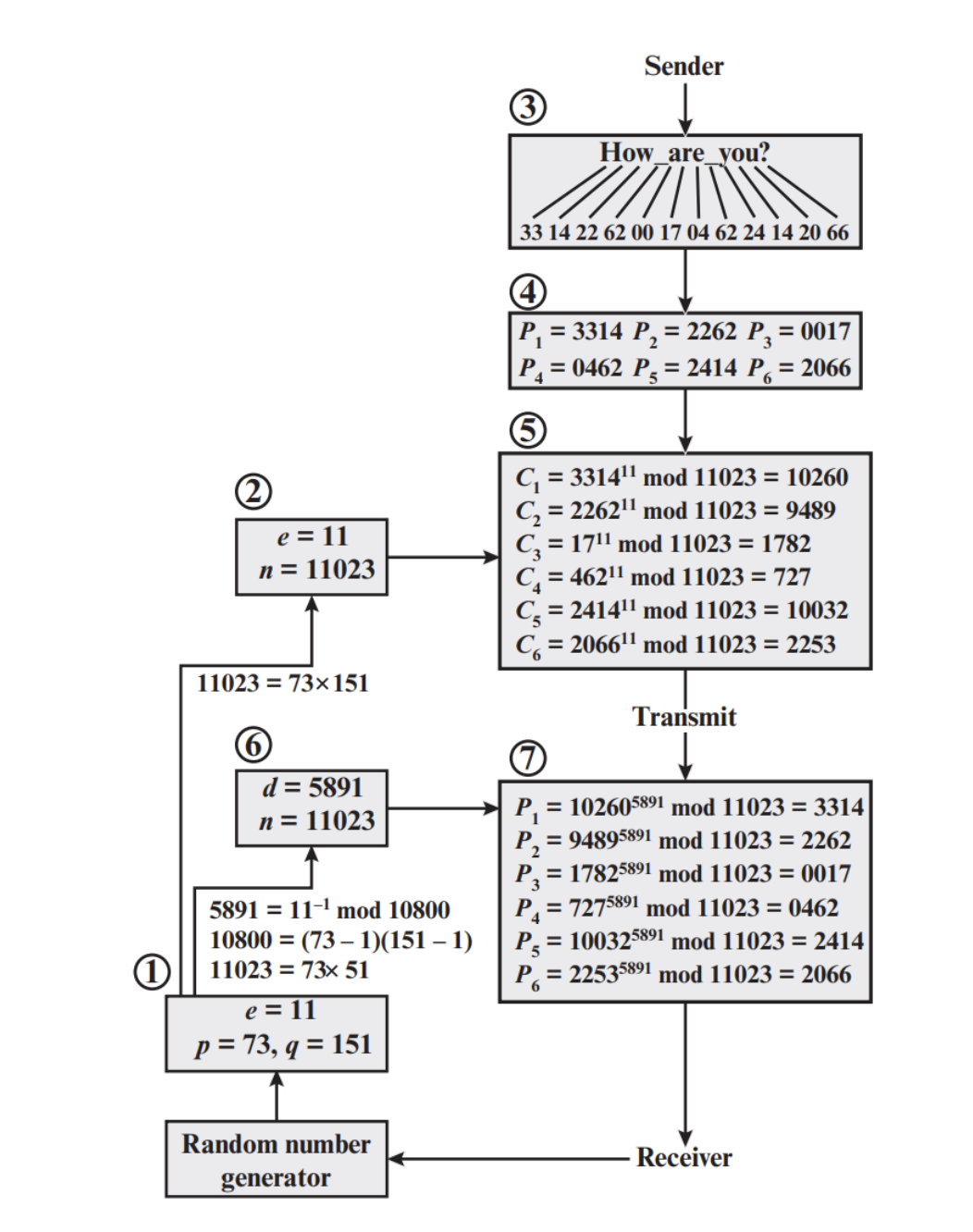
1. Two prime numbers $p$ and $q$ Come up with $p$ and $q$, where $p$ and $q$ are extremely large prime numbers (greater than 2048 bits) and they cannot be to close to each other.
2. Calculate $n$ The number $n$ is calculated as $n=p\times q$
3. Calculate the $\varphi (n)$ Calculate the Euler’s phi of $n$. Where $\varphi (n)=(q-1)(p-1)$.
4. Choose the encryption key $e$ (public key) The encryption key $e$ follows the conditions that $e\{\begin{array}{l}1<e<\varphi (n)\\ gcd(e,\varphi (n))=1\end{array}$ The second condition suggests that $e$ has to be co-prime with $\varphi (n)$, which means $e$ cannot share any factor of $\varphi (n)$.
5. Calculate the decryption key $d$ (private key) The $d$ is deterministic once $\varphi (n)$ and $e$ is obtained. The equation to calculate $d$ can be described as below. $de(mod\varphi (n))=1$ And it can be rearranged to: $d\equiv e^{-1}(mod\varphi (n))$
6. Public key $Ke{y}_{Pub}=(e,n)$
7. Private key $Ke{y}_{Pri}=(d,n)$

After the key generation, all $p$, $q$, and $\varphi (n)$ have to be permanently deleted for prevent reconstruction. The number $n$ is a public information.

Encryption

Encryption by Bob with Alice’s public key. Plaintext: $M<n$ Ciphertext: $C=M^e\mathrm{mod}n$

Decryption

Decryption by Alice with Alice’s private key. Ciphertext: $C$ Plaintext: $M=C^d\mathrm{mod}n$

Number mapping

The RSA algorithm can only encrypt numbers. Therefore, letters have to be mapped to numbers before they can be encrypted. The letter a maps to 1, and the letter b maps to 2…

Security of RSA

The RSA algorithm make use of the trapdoor property. The security of RSA rests on

• Obtaining the $e^{th}$ root is computationally infeasible unless you know $d$.
• Factoring $n=qp$ is computationally infeasible for large primes.

If an attacker could factor $n$ into $p$ and $q$, they could easily compute $\varphi (n)=(p-1)(q-1)$ and use it to calculate $d$ from $e$. However, if $p$ and $q$ are large and randomly chosen, factoring them is considered computationally infeasible with current technology.

To maintain the security of RSA

• $p$ and $q$, $p\ne q$ must be very large (greater than 2048 bits)
• $p$ and $q$, $p\ne q$ must not be too close together (allows forms fast factoring)
• Never implement RSA yourself and use in production

Attacks on RSA

• Brute force
  • Trying all possible private keys
• Mathematical attacks
  • Approaches to factoring the product of two primes
• Timing attacks
  • Attacker monitors how long each RSA operation takes and use this information to infer bits of the private key, Using constant-time algorithms that perform computations in the same amount of time regardless of the input values
• Hardware fault-based attack
  • Inducing hardware faults in the processor that is generating digital signatures.
• Chosen ciphertext attack
  • The attacker choses a specific ciphertext and observe the corresponding decrypted plaintext. This allows them to exploit the structure of the RSA, especially RSA that is malleable or improperly implemented.

Malleability of RSA

RSA is not secure to use without padding

The malleability of RSA allows attacker to manipulate the encrypted messages without needing to know the actual contents of the original message. The malleability of RSA arises because of its mathematical structure. As the working out earlier, the RSA encryption can be described as: $C=M^e\mathrm{mod}n$ Where

• $M$ is the plaintext message
• $e$ is the public exponent
• $n$ is the modulus (product of two large prime numbers $p$ and $q$)
• $C$ is the resulting ciphertext

Chosen Ciphertext Attack (CCA)

If an attacker intercepts a ciphertext $C$ and wants to generate a new ciphertext $C^{\prime }$ such that the decrypted plaintext $M^{\prime }$ is a known transformation of the original plaintext $M$, they could exploit RSA’s malleability as follows: If the attacker multiplies the plaintext by a random factor $r^e$, they get: $C^{\prime }=C\cdot r^e\mathrm{mod}n=(M^e\cdot r^e)\mathrm{mod}n=(M\cdot r{)}^e\mathrm{mod}n$ When $C^{\prime }$ is deciphered by the receiver, the plaintext becomes $M\cdot r$ . The receiver then ask the sender (attacker) that what does the plaintext mean? The attacker can take the plaintext and divide it by $r$ to obtain the original message $M$.

Padding

The malleability of RSA is considered a weakness because it allows unauthorised manipulation of messages. To address this, secure implementations of RSA use padding schemes like OAEP (Optimal Asymmetric Encryption Padding) that adds more randomness on encryption and removes it on decryption.

Hybrid encryption

Almost all public-key encryption uses hybrid encryption in practice.

Problems with RSA

Public-key cryptography is slow

RSA replies on the exponentiation of large numbers, and performing arithmetic operations on large integers, which makes it computationally expensive compared to symmetric cryptographic algorithm like Advanced Encryption Standard (AES). RSA is 100-1000 times slower than AES.

Mapping numbers to characters

RSA works with numbers, so characters must be converted into numerical representation, this process has impact on the RSA performance. It involves encoding the text in a form that RSA can work with (mentioned in number mapping).

The use of hybrid encryption

Hybrid encryption combines the strengths of both asymmetric and symmetric encryption to overcome the limitations of RSA performance in continuous encryption. In hybrid encryption:

• Asymmetric encryption: Used to securely exchange a symmetric key.
• Symmetric encryption: Used to efficiently encrypt and decrypt actual data in communication.

---

Back to parent page: Network Security and Cryptography