Maxima Set

Related paradigm:

• Divide and Conquer

AlgorithmDivide_and_ConquerMaxima_Set

---

Maxima set problem is to identify the set of maximum points in a 2D plane.

Definition: A point is maximum in a set if all other points in the set have either a smaller x or smaller y coordinate.

Problem: Given a set S of $n$ distinct points in the plane, find the set of all maximum points.

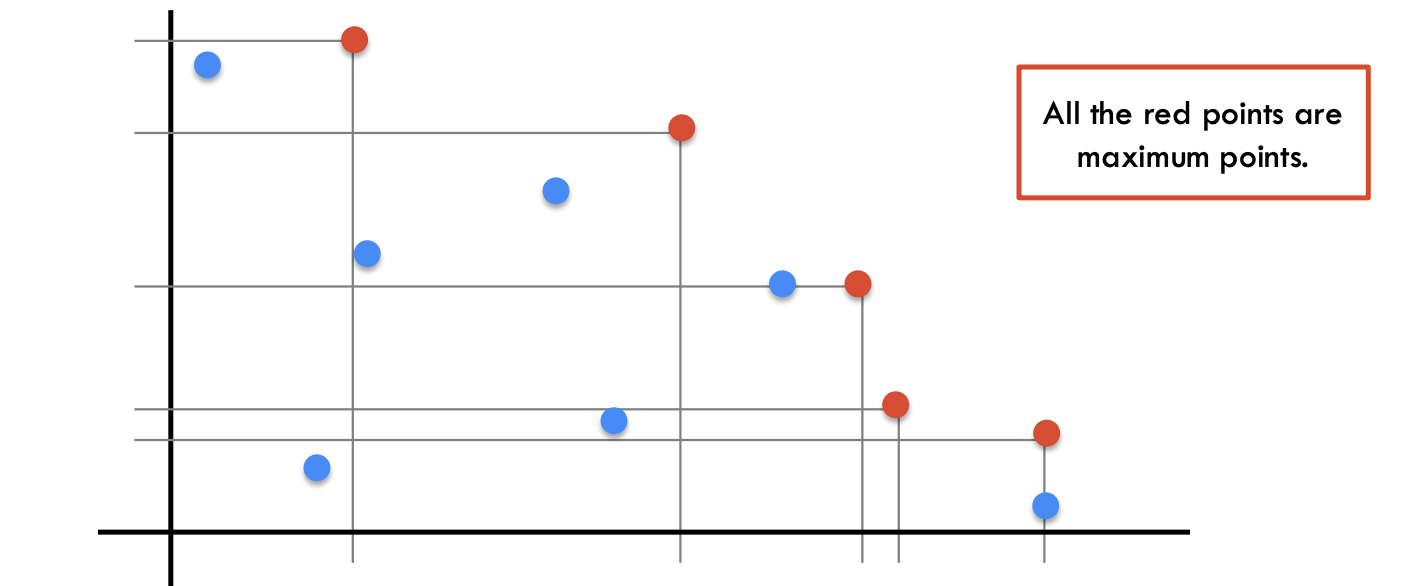
This problem can be solved using divide and conquer paradigm for better runtime time efficiency.

• Preprocessing
  • Sort the points by increasing x coordinate and store them in an array or list. This ensures when dividing the points, the left sub list contains points with smaller x-coordinates, and right sub list contains with larger x-coordinates.
• Divide
  • Split the sorted list into two halves, let $P_l$ be the left half and $P_r$ be the right half
• Conquer
  • Recursively find the maxima set for $P_l$ and $P_r$
  • Base case is reached when the input list has only one point, it is returned as is because a single point is trivially a maxima
• Merge
  • Find the highest point in the $P_r$(point with the maximum y-coordinate) by sorting the list by their y-coordinate.
  • Each point in the $P_l$ is compared with the highest point in the $P_r$. If a point in the left set $P_l$ has a greater y-coordinate (higher than the highest point in the right set), the point is included in the resulting list.
  • Finally, all points from the $P_r$ are added to the resulting list.

Implementation

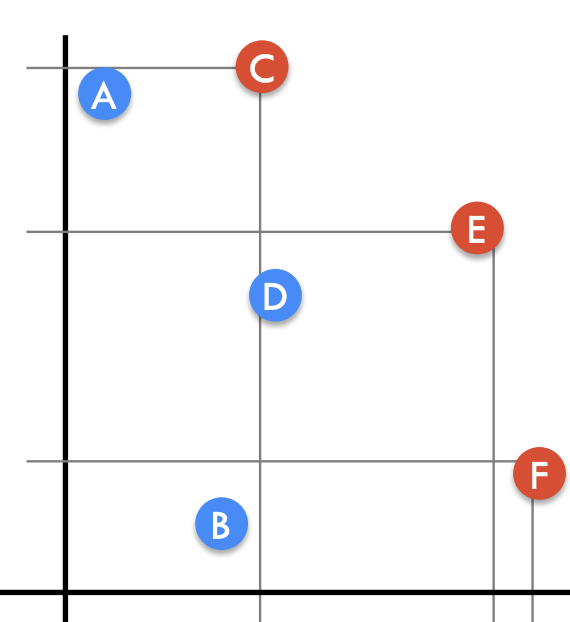
Given a 2D plane with points allocated, the points in red are the resulting maxima points.

 /* This implementation assumes the points are added in ascending order of their x coordinate */  
    public static void main(String[] args) {  
        List<Point> points = new ArrayList<>();  
        points.add(new Point(1, 6)); //A  
        points.add(new Point(3, 2)); //B  
        points.add(new Point(4, 7)); //C  
        points.add(new Point(5, 4)); //D  
        points.add(new Point(7, 5)); //E  
        points.add(new Point(8, 3)); //F  
        
        List<Point> maxima = findMaxima(points);  
        for (Point pt : maxima) {  
            System.out.println(pt);  
        }  
    }  
    
    public static List findMaxima(List<Point> input) {  
        if (input.size() <= 1) {  
            return new ArrayList(input);  
        }  
        int mid = input.size()/2;  
        List<Point> left = new ArrayList<>(input.subList(0, mid));  
        List<Point> right = new ArrayList<>(input.subList(mid, input.size()));  
        
        // recursively find maxima in the left and right set  
        List<Point> leftMaxima = findMaxima(left);  
        List<Point> rightMaxima = findMaxima(right);  
        return merge(leftMaxima, rightMaxima);  
    }  
    
    public static List<Point> merge(List<Point> left, List<Point> right) {  
        List<Point> mergedSet = new ArrayList<>();  
        Collections.sort(right, Comparator.comparingInt(Point::getY));  
        Point highestPtInRight = right.get(right.size()-1);  
        // if any point in the left is higher than the highest point in the right  
        // add it to the resulting list        
        for(Point pt : left) {  
            if (pt.getY() > highestPtInRight.getY()) {  
                mergedSet.add(pt);  
            }  
        }  
        // add all points in the right to the resulting list  
        mergedSet.addAll(right);  
        return mergedSet;  
    }  
}

Correctness

The input is divided into two halves $P_l$ and $P_r$, since every point in the original set is either in the left or right half, any point in the overall maxima set must be in either $P_l$ or $P_r$. The highest point in the right set $P_r$ has the maximum y coordinate among all points in the right set. By comparing each point in the left set $P_l$ with the highest point in the right set $P_r$, if a point in $P_l$ has greater y coordinate value, then the point is not dominated by this highest point, which can be further concluded it is not dominated by any other point in the $P_r$ because no other point in the right set has a higher y coordinate value.

Time complexity

The algorithm time complexity can be analysed using master theorem.

• Divide the problem
  • The input list is divided into 2 halves ($a=2$), each of size $\frac{n}{2}$ ($b=2$).
• Combine the result
  • The merge step involves combing the results from left and right halves, the operation takes $O(n)$ time as it involves sorting and linear scan ($f(n)=O(n)$).

Given the master theorem for divide and conquer in general form: $T(n)=a\times T(\frac{n}{b})+f(n)$ From the evaluated result:

• $a=2$
• $b=2$
• $f(n)=n$

We can obtain the resulting expression: $T(n)=2T(\frac{n}{2})+n$ Analyse the master theorem equation:

• Non-recursive part growth rate: $f(n)=n$, $c=1$
• Recursive part growth rate: ${\log }_{b}a={\log }_{2}2=1$

The non-recursive part and recursive part have the same growth rate since $c={\log }_{b}a$. The overall time complexity is: $T(n)=n\log n$

---

Back to parent node: Divide and Conquer