Abstract data type:

ADT - Binary Tree

Data_Structure Tree Binary_Tree Balanced_Tree Binary_Search_Tree AVL_Tree

An AVL (Adelson-Velsky Landis) tree is a self-balancing Binary Search Tree (BST) where the balancing factor (bf) of nodes is in rage of {-1, 0, 1}, which means the difference between heights of left and right subtree for any node cannot be more than one. An AVL tree always have $O (lo g n)$ for searching, insertion, and deletion.

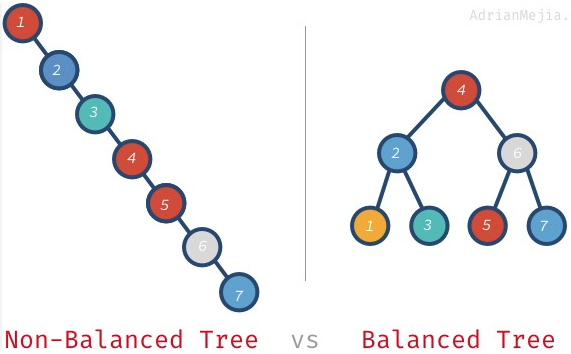
Properties

AVL trees are self-balancing BSTs
Each node in an AVL tree has at most two children
The tree has all the properties of a BST with the subtree of a node cannot be greater than the value of the subtree, vice versa.
Balancing factor (bf)
- The balancing factor is defined as $b f = height of left subtree - height of right subtree$
- In AVL trees, the balancing factor cannot be less than -1 or greater than 1
- $∣ b f ∣ = ∣ height of left subtree - height of right subtree ∣ \leq 1$ for all nodes in the AVL tree

Pros and cons

Advantage
- Searching, insertion, and deletion are always in $O (lo g n)$ time
- The height balancing adds no more than a constant factor to the speed of insertion
Disadvantage
- Difficult to program and debug
- Extra space for balance factor
- Most large searches are done in database systems uses other structures (e.g. B-tree)

Implementation

Balancing factor (bf)

Balancing factor of a node is calculated as the difference in height between its left and right subtrees. The expression can be described as: $b f = height of left subtree - height of right subtree$ Before determine the balancing factor of a node, we need to know the height of a subtree. If a node does not have any child, the height of its subtree is -1 (define the height of an empty tree as -1).

Interpretate balancing factor

Balancing factor (bf)	Description
$b f = 0$	Perfectly balanced
$b f = 1$	Left subtree is 1 level taller than the right subtree
$b d = - 1$	Right subtree is 1 level taller than the left subtree
$b f > 1$	Unbalanced tree, with heavy left subtree
$b f < 1$	Unbalanced tree, with heavy right subtree

Height and balancing factor

The balancing factor is calculated based on the heights of the subtrees. The heigh of a subtree is equivalent to the height of the root node of that subtree. The height of a node is set to 0 initially when the node is created. As the tree grows and rebalancing operations are performed, the heights of nodes are updated accordingly. (see [[#|insert method]]) The height of a node can be evaluated as: $Height (N o d e) = max (Height (LeftChild, RightChild) + 1)$ The height of a node is defined as the maximum heigh of its children plus 1.

In this example, the heights of the nodes are:

Node 10: 0
Node 20: 1
Node 40: 0
Node 30: 2

When a new node 5 is inserted

Heigh of node 5 upon insertion is 0. Backtrack and update heights:

Node 10 new height : $ma x (0, - 1) + 1 = 1$
Node 20 new height: $ma x (1, 0) + 1 = 2$
Node 30 new height: $ma x (2, 0) + 1 = 3$

Balance the tree: Check balance factors:

Balance factor of node 30: $b f = 2 - 0 = 2$
Unbalanced, with heavy left subtree
Right rotation will be performed (will be discussed next)

class TreeNode {
	int value, height;
	TreeNode(int val) {
		value = val;
		height = 0;
	}
}
 
// get height of a tree node
int height(TreeNode node) {
	if (n == null)
		// height of an empty tree is -1
		return -1;
	return node.height;
}
 
void updateHeight(TreeNode node) {
	node.height = Math.max(height(node.left), height(node.right)) + 1; 
}
 
int balanceFactor(TreeNode node) {
	if (n == null)
		return 0;
	return height(node.left) - height(node.right);
}

Rotations

The characteristic feature of an AVL tree is the rotation operation. It allows AVL tree to maintain balance while preserving BST property. When a node has a balancing factor $> 1$ , it is an unbalanced node. Depend on what type of imbalance, employ different rotation strategy: right rotation, left rotation, right-left rotation, and left-right rotation.

Right rotation

Right rotation is performed when a node is unbalanced, and has become left heavy (its left subtree is taller than its right subtree for more than 1 level). It takes the root node (unbalanced node) and rotates it to the right.

Before Rotation
        30
       /  
      20   
     /  \  
    10  null

Node 30 has a balancing factor of 2 (height difference of 2 between its left and right subtree) We perform the right rotation:

20: The left child of the root node (30) becomes the new root
The right child of 20 becomes the left child of the old node (30) after rotation
10: The original left child of 20 remains as the as the left child of the new root (20)

After Rotation
      20
     /  \
    10   30
        /
      null

TreeNode rightRotate(TreeNode node) {
	TreeNode child = node.left; // 20
	TreeNode grandChild = child.right; // null
	
	// rotate node to the right around child
	child.right = node;
	node.left = grandChild;
	
	// update heights
	updateHeight(node);
	updateHeight(child);
	
	// return the new root node
	return child;
}

Left rotation

Left rotation is performed when a node is right heavy. It takes the root node and rotates it to the left.

Before Rotation
		10
	      \
	       20
	      /  \
	     15   22

We perform the left rotation:

20: The right child of the root node (10) becomes the new root
15: The left child of 20 becomes the right child of the old root node (10) after rotation
22: The original right child of 20 remains as the right child of the new root (20)

After Rotation
		20
	   /  \
	  10   22
	    \
	     15

TreeNode leftRotate(TreeNode node) {
	TreeNode child = node.right; // 20
	TreeNode grandChild = child.left; // 15
	
	child.left = node; 
	node.right = grandChild;
	
	updateHeight(node);
	updateHeight(child);
	
	return child;
}

Right-left rotation

Right-left rotation is performed when a node is right-heavy (bf < -1) and its right child is left-heavy (bf > 0).

Before Rotation
	  10
		\
		 30
		/
	   20

We perform the right then left rotation:

Perform a right rotation on the right child of the root node (30)
Perform a left rotation on the unbalanced node (10)

Right Rotation 
      10
        \
         20
           \
            30

Left rotation
      20
     /  \
    10   30

node.right = rightRotate(node.right) // 30
leftRotate(node) // 10

Left-right rotation

Left-right rotation is performed when a node is left heavy (bf > 1) and its child is right heavy (bf < 0)

Before Rotation
      30
     /
   20
     \
     25

We perform the left then right rotation:

Perform a left rotation of on the left child of the root node (20)
Perform a right rotation on the unbalanced node (30)

Left Rotation
      30
     /
   25
   /
 20

Right Rotaion
      25
     /  \
   20    30

node.left = rightRotate(node.left) // 20
leftRotate(node) // 30

Rotation cases

bf of unbalanced node	bf of child node	Choice of rotation
$b f > 1$ (left-heavy tree)	$b f \geq 0$	Right rotation
$b f < - 1$ (right-heavy tree)	$b f \leq 0$	Left rotation
$b f > 1$ (left-heavy tree)	$b f < 0$ (right-tilted tree)	Left-right rotation
$b f < - 1$ (right-heavy tree)	$b f > 0$ (left-tilted tree)	Right-left rotation
![[Pasted image 20240601015322.png	600]]
The rotation operation can be encapsulated into a single method.

// perform rotation to restore balance of a bst
TreeNode rotate(TreeNode node) {
    // get the balance factor of node
    int balanceFactor = balanceFactor(node);
    // left-heavy tree
    if (balanceFactor > 1) {
        if (balanceFactor(node.left) >= 0) {
            // only right rotation
            return rightRotate(node);
        } else {
            // left then right rotation
            node.left = leftRotate(node.left);
            return rightRotate(node);
        }
    }
    // right-heavy tree
    if (balanceFactor < -1) {
        if (balanceFactor(node.right) <= 0) {
            // only left rotation
            return leftRotate(node);
        } else {
            // right then left rotation
            node.right = rightRotate(node.right);
            return leftRotate(node);
        }
    }
    // balanced tree, no further rotation needed
    return node;
}

Insert

The insert operation in AVL trees is similar to BST insertion. The only difference is the AVL tree performs rotation on node after insertion if necessary, and update the height and balancing factors of nodes.

void insert(int val) {
    root = insertHelper(root, val);
}
 
TreeNode insertHelper(TreeNode node, int val) {
	//check the root of current subtree
    if (node == null)
	    //indicating an empty subtree, the new node is assigned to                  //the root of this subtree
        return new TreeNode(val);
    if (val < node.value)
		//update the left child of the current node with the result of 
	    //the insertion operation
        node.left = insertHelper(node.left, val);
    else if (val > node.value)
        node.right = insertHelper(node.right, val);
    else
        return node; // do not insert duplicate nodes
    
    // update the height 
    updateHeight(node); 
    // perform rotation operation to restore balance to the subtree 
    node = rotate(node);
    // return the root node of the subtree
    return node;
}

Remove

The remove is inherited from BST remove method, with additional rotation and update attribute operations.

void remove(int val) {
    root = removeHelper(root, val);
}
 
TreeNode removeHelper(TreeNode node, int val) {
    if (node == null)
        return null;
    // find and remove the node 
    if (val < node.value)
        node.left = removeHelper(node.left, val);
    else if (val > node.value)
        node.right = removeHelper(node.right, val);
    else {
        if (node.left == null || node.right == null) {
            TreeNode child = node.left != null ? node.left : node.right;
            if (child == null)
                return null;
            else
                node = child;
        } else {
            TreeNode temp = node.right;
            while (temp.left != null) {
                temp = temp.left;
            }
            node.right = removeHelper(node.right, temp.val);
            node.val = temp.val;
        }
    }
    // update node height, restore balance if needed
    updateHeight(node);
    node = rotate(node);
    return node;
}

Back to parent page: Data Structures and Algorithms

Reference

Computer Science Wiki

Explorer

AVL Tree